United States News
See other United States News Articles
Title: Forensic acoustic proof of SECOND shooter in the Las Vegas massacre
Source:
[None]
URL Source: https://www.youtube.com/watch?v=JxmEFeKy8aI
Published: Oct 11, 2017
Author: Mike Adams TheHealthRanger
Post Date: 2017-10-11 00:40:47 by A K A Stone
Keywords: None
Views: 56439
Comments: 148
Post Comment Private Reply Ignore Thread
Top • Page Up • Full Thread • Page Down • Bottom/Latest
Begin Trace Mode for Comment # 141.
#1. To: nolu chan, VXH, buckeroo, tooconservative, cz82, redleghunter (#0)
Found this interesting video.
Adams assumes a shooter using an AR-15 with .223 Remington 55 grain ammo. He states 20% humidity. He states a 925 m/s bullet velocity which is ~3034.8 fps. He specifies a 16.5" barrel, but a 3034.8 fps initial velocity would seem to indicate a 20" barrel or different ammo. I believe the white board has an error. The flight time should be 0.532s, not 0.528s. It lists both the 400 yard flight time and the lag time as 0.528s. This would mean the bullet velocity was precisely double the speed of sound, and that double 0.528s, or 1.056s would be the 400 yard travel time for the speed of sound. The time of sound travel for 400 yards at 1130 fps is 1.062. http://gundata.org/blog/post/223-ballistics-chart/ He cites his use of a gundata ballistics chart for travel time. gundata indicates for 400 yards, the time of travel is 5.32s, specifying a standard 55gr Remington .223 bullet leaving the barrel at 3,215fps. Adams also specified a 16.5 inch barrel, but it seems an AR-15 with a 16.5 barrel does not achieve 3,215 initial velocity. Testing with different barrel lengths indicates an AR-15, 16.5" barrel, with Remington .223 ammo, does not achieve 3,034.8 muzzle ("initial") velocity. With a 20" barrel, the same setup gets 3,071 fps muzzle velocity. A 25" barrel gets it up to 3,221 fps muzzle velocity. A 16.5" with Federal M193/55 gets 3,187 fps muzzle velocity. http://guide.sportsmansguide.com/ballistic-chart/remington_charts/223rembal.htm A ballistics chart indicates that a Remington .223 will not get the stated bullet velocity. Assuming the shots were fired from room 32135, and that end of the Mandalay Bay Hotel was 1208 feet from the base of the bandstand, and that a bullet struck the pavement at or near the base of the bandstand, the long side a right triangle would be 1208 feet and the short side would be the height of room 32135. The building claims a height of 480 feet and 44 stories, for an average of 10.91 feet per story. The 32nd floor would be 338.21 feet up. (31 x 10.91, base of floor 1 has zero height). With sides of 1208 and 338.21, the hypotenuse would be 1254.45 feet. The actual distance the bullet traveled would be more than that as it would not follow a straight path, but would follow an arc. Using estimates of distance to striking the venue surface of ~1250 feet, and detected lag times of 0.559 sec and 0.374 sec, the slower bullet made the 0.374 lag time; the faster bullet arrived .559 sec before the muzzle blast. At 1130 fps, the sound would cover 1250 feet in about 1.106 seconds. A bullet making the 1250 ft trip .559 sec before the sound, made the trip in .547 sec. A bullet making the 1250 ft trip .374 sec before the sound, made the trip in .732 sec. 1250 feet in .547 sec is an avg velocity of ~2236 fps. 1250 feet in .732 sec is an avg velocity of ~1708 fps. This assumes both shots were taken from the same location. What bullets were used can be ascertained by collecting the bullets. What was left in the room should be inventoried, along with what guns were in the room. http://onyourownadventures.com/hunttalk/showthread.php?267715-308-Ammo-Help/page2 Most mfgs recommend a minimum velocity of 1800 fps for proper expansion. The so called "magic number" associate with elk hunting is 1200 lb ft Energy. Below that is risky and I prefer 1400 lb ft as my personal standard. Although every gun is different the ammo mfg. Will put their tested numbers out for their loads. According to Federal their TBT 165 gr out of a 308 maintains 1939 fps and 1377 lb ft at 500 yards. Mathematically that should do the job as long as the bullet hits it's mark. Federal lists the same weight game King at 1708 FPS and 1069 ft lb at 500 yards. Obviously not the best option. If you keep 400 yards and in either a 150 or 165 gr factory loaded bonded round should work fine on elk. You just need to find the one that goes exactly where you want it to every time you press the trigger. This would suggest the possibility of the 1708 fps round being a .308 (or whatever else gets around 1708 fps at 400 - 450 yards. http://gundata.org/blog/post/223-ballistics-chart/ [...] .223 Remington, Remington Metal Case, 55gr. 400 yards This ballistics chart indicates .532 seconds for 400 yards, at 1588 velocity. .532 seconds would indicate 2255.6 average velocity for the 400 yards, and the velocity of the bullet leaving the barrel is specified at 3215 fps.
All numbers he pulled out of his arse? Plus there's the little problem that he doesn't present any actual audio evidence.
Plus there's the little problem that he doesn't present any actual audio evidence. The audio he used is presented. Your chartoon is an absurdity.
LOL. He scribbled on a whiteboard. The amplitude graphs of the audio referenced on my meme can be reproduced by anyone with minimal tools. It's REPRODUCIBLE - that's what differentiates valid science from conspiratorial buffoonery. Show us the actual amplitude graphs or STFU.
That you reproduce meaningless bullshit is meaningful, but not as you intend.
The amplitude graphs are reproducible by anyone who has simple tools and access to the video on Youtube. Where's yours?
Proving imbeciles can reproduce. As the U.S. Supreme Court observed, "Three generations of imbeciles are enough." Your chartoons, with your hilarious analysis, are entertaining, sort of like the scientific sounding youtubers preaching flat Earth theory.
The amplitude graphs are reproducible by anyone who has simple tools and access to the video on Youtube. Where's yours? { shrug } Maybe you just don't have what it takes.
On your spreadsheet chartoon, notice that you calculate T = Tb - Ts. You calculate elapsed time as the time it took the bullet to travel, minus the time it took the sound to travel. As the bullet is supersonic, and sound is a constant, the sound would travel 400 yards in 1.06s and the bullet would travel the 400 yards in less than 1.06s. Subtracting 1.06 from a smaller number will always yield a negative number. At 1200 feet, you actually calculate Tb as 0.448578s, and Ts as 1.062s and calculate the T as -0.6126, negative 0.6126 seconds. The average donkey could recognize that something is wrong when the result is negative time. Just what do you think happens in negative 0.6126 seconds? You could at least recognize that if you get a negative number, you have stated the required formula backwards, and you proceeded to perform the calculation backwards, and present the bass ackwards result of your understanding of the study you looked at. You've got what it takes to make bullets travel in negative time. Your brain apparently has zero amplitude.
>>at 1200 feet, you actually calculate Tb as 0.448578s, and Ts as 1.062s and calculate the T as -0.6126, negative 0.6126 seconds. 0.448578 is the ballistic projectile time. 1.062 is the time to travel the same distance at the speed of sound The MEASURED, absolute value, of the Ellapsed Time difference, per the audio amplitude graph... ...between the Last Bullet sound event and the Last Report sound event is 0.689655 Now, ask your donkey - what distance does that MEASURED absolute time difference correspond to on the chart?
No Absolute value is ever expressed as a negative number. Had your undisclosed formula for the last column of your spreadsheet included code to express an absolute value, your spreadsheet results would not appear as negative numbers. But your spreadsheet displays negative numbers and you did not even question it or fix your spreadsheet. The results should all be positive, like this: d = distance 400 yards, 1200 feet Column 1 = d/FPS = time in seconds Row 1 = directly inserted data. Data display is set to show 3 decimal places. Row 2 = spreadsheet formulas The formulas for Row 2 are dragged down to generate Rows 3-30.
>>No Absolute value is ever expressed as a negative number. =========== Since we KNOW from the observed audio Vb is supersonic, we can treat the difference between Tb and Ts as Absolute. Range corresponds to the ABSOLUTE value of the difference in time.
I know. They have a spreadsheet function for that. It has been around since Lotus 123 and Quatro. ABS(number).
Yes, but in this case the ABS is implied in knowledge of what the spreadsheet is actually calculating. If you applied ABS(Tb-Ts-) the chart would loose the information regarding whether the Vb was super-sonic or not, which the negative numbers conveniently tell us. The author's formula works just fine without your tweakage. http://ww w.btgresearch.org/AcousticReconstruction02042012.pdf And that IS the same formula I have in my illustration:
Why do you keep posting this chartoon when all your data is not only wrong, but farcical? The only things you proved is that you do not know how to calculate the average velocity of an imaginary bullet and you are hopeless at spreadsheets. Your entertainment value as a useful idiot is over for now, and you will never figure it out without more help. Help is on the way, grasshopper. Columns 1, 2, and 3 are direct entry of data generated by entering imaginary data into a generator at http://www.shooterscalculator.com/. I replicated the data taken from the calculator with “My BB's.” If I input initial velocity as 3240 fps, and other data, and call it “My BB's,” I can show a chart for magical bb’s. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 The Shooter’s Calculator only provides a result based on user input. It does not present a spreadsheet with the formulas to generate the data. The data from the Calculator can be cut and pasted into a spreadsheet, or entered by direct entry; this produces data in the cells, but no spreadsheet formulas in the cells. The chart states the speed of sound as 1130 feet per second (fps). The remaining 4 columns, (4, 5, 6, 7) were generated by VxH. Column 6 uses 1130.8 fps to calculate the time for sound to travel the distance stated in Column 1. Column 4 is labeled as (Avg V) Vb. This column purports to present the average velocity of the bullet to cover the distance for the row it is in. All of the data in this column is epically wrong as the methodology of calculation is absurdly wrong. To calculate the average velocity of the bullet, divide distance by time. Instead of this, a personal misbegotten formula was used. Probably a pocket calculator for each cell in Column 4 was used to perform the calculations, and the data was directly entered into the cells by hand. For the first two data rows, sum 3240 and 3163 and divide by 2. 6403/2 yields the 3201 in Column 4. For the first three data rows, sum 3240+3163+3088 for 9491. 9491 / 3 yields the 3163.6667 in Column 4. And so on, and so forth. All the calculated Column 4 data (average Vb), is garbage. The chosen methodology was to sum the velocity given for each distance, and divide by the number of elements summed. This produces nonsensical data. Example: You drive a car 100 miles at 80 mph. You drive another 100 miles at 20 mph. With this bogus methodology, 80 + 20 = 100, divide by 2, and your average velocity was 50 mph. Not. In the real world, you drove 100/80 or 1.25 hours at 80 mph. You drove 100/20 or 5 hours at 20 mph. And you drove 200 miles in 6.25 hours. Your average speed was 200/6.25, or 32 mph. Column 4, in addition to using an absurd methodology for its calculations, also incorporates two summing errors for the velocities taken from Column 3, at 900 feet and 1275 ft. In each case, the actual sum was 1 less than that calculated. Spreadsheet formulas are not prone to fat finger syndrome, and do not make such errors, but someone with a pocket calculator or pen and paper does. The data was typed in after external calculation. Where you calculate 2367.5926 average Vb at 1950 feet, 1950/1.211933 (the velocity of the bullet in Column 5), it yields 1608.9998 fps, remarkably close to the 1609 in Column 3. But then, the elapsed time in Column 2 is 0.86, not 1.21933. It is a conundrum how the bullet traveled for 1.21933 seconds in an elapsed time of 0.86 seconds. Of course, when you use Column 1 1950 ft and Column 3 1609 fps to derive the time of flight, the formula is d/Vb, and Vb is the Average Velocity. The bullet will travel 1905 feet distance (Col 1) in 0.86 sec time (Col 2) in 1905/0.86 or 2267.4418 average Vb. Stated in your headnote is Tb is d/Vb. It is noteworthy that you used Column 3 as the "average" velocity of the bullet in order to derive the other average velocity of the bullet in Column 4. Column 5 (Tb) incorporates the garbage data from Column 4 into its calculations, and all the resulting calculated data is wrong. GIGO. Column 7 (T = Tb – Ts) incorporates the garbage data from Column 5 and all the calculated data is wrong. GIGO. The chart is multicolor and pretty, but the data for the imaginary bullet is demonstrably wrong in every column you created, except for column 6 where you succeeded in dividing the distance by 1130.8.
>> and the data was directly entered into the cells by hand. Bzzzt. Fail again.
Bzzzt. Fail again. Nope. You said you created spreadsheet and used their formulas. Had you used their formulas you would not have bullshit results, including arithmetic errors in the columns. Which formula of theirs did you use to manufacture the wrong bullet velocities? Cite any source that says to find average velocity with the method you used. When you introduced this bullshit on the other thread at your #19 to A K A Stone, you said: https://libertysflame.com/cgi-bin/readart.cgi?ArtNum=53046&Disp=19#C19 Only you did not use their formulas or you would not have gotten all the data you derived bass ackwards wrong, and you did not create formulas and drag them down through the rows, or you would not have the calculation errors the are apparent. I created a spreadsheet using the same data and created formulas and dragged them down through the rows. They work. That is how I can pinpoint where you made calculating errors in your data entry. All you did was cut and paste the chart data into a spreadsheet workbook. Columns 1 thru 3 were cut and paste. For Column 4, there is no chance that you created a formula and dragged it down through the rows. You go off at range 900 where you summed to 36497 instead of 36496. This error of 1 continues through to range 1275, where you summed to 47,572 instead of 45,570. This put the summing error at 2, which continued through range 1950 where you ended. This is not a spreadsheet error. I used two different formulas to sum the velocities, with results identical to each other. You used no formula. You sat there with your pocket calculator and added the first two and typed in the result. Then you added the third velocity and typed in the result. And you did this for each data entry in that column. If you have any spreadsheet formula that can replicate your results, produce it. As Column 4 calculates the sum of the velocities divided by the number of velocities, and the sum of the velocities was not created by a formula on a spreadsheet column, the column was manual data entry. In Column 5, d/Vb, the distance is correctly divided by the bogus average velocity, yielding a bogus result. When it is as simple as programming one column divided by another, good job. When it is summing a changing number of rows, fuhgetaboutit. That was direct data entry with arithmetic errors. In Column 6, I stated you were able to divide distance by 1130.8. When it is summing a changing number of rows, fuhgetaboutit. That was direct data entry with arithmetic errors. In Column 7, you managed to correctly subtract the bogus data in Column 5 from the bogus data in Column 6, yielding all bogus results. When it is as simple as programming one column subtracted from another, good job. It should have included an ABS function to avoid getting negative time results.When it is summing a changing number of rows, fuhgetaboutit. That was direct data entry with arithmetic errors. As Columns 5 and 7 incorporate the brain dead data in Column 4, with a double whammy of a bogus formula and calculation errors, all data in Columns 5 and 7 is bogus. Your chart in Column 2 from btgresearch indicates Tb for range 1950 is 0.86 seconds. Column 5 for 1950 range indicates Tb is 0.823621. You call that fixing a rounding error???? How did displaying only two decimal places to 0.86 convert to 0.823621????
As Column 4 calculates the sum of the velocities divided by the number of velocities, and the sum of the velocities was not created by a formula on a spreadsheet column, the column was manual data entry. Bzzzt. Another Nolu-FAIL. =SUM(C9:C10)/L9 Now please tell us how Nolu-Time works and then explain why the values of Column J are closer to Time (Column B) than Nolu-Time(Column I)? "more accurate is to divide the distance by the velocity and get the time to more decimal places nolu chan posted on 2017-10-28 18:47:52 ET https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53025&Disp=153#C153
Chan is kicking your ass and you are looking foolish with all your errors.
Says the genius who posts videos with scribbling on a whiteboard presented as "PROOF". Can you solve for T given a 75 foot vector having Vmin and Vmax? Let's see if Noluchan's donkey can!
Post some more goofy Klingon pics It enhances your credibility.
My Klingon pics succinctly illustrate the gullible nature of individuals who post videos with scribbling on a white board as "proof". How's that workin' for ya? Meanwhile: Q: Can you solve for T given a 75 foot vector having Vmin and Vmax?
You have repeatedly changed and modified your numbers. Could you provide me a list of all of your errors that you posted so I can remove them from the site so people don't look at bullshit?
Truth is great and will prevail unless deprived of her natural weapons, free argument and debate. Does that work in AKA Stoned Land? There's nothing wrong with refining an analysis in the context of an honest desire to seek the truth. Time is still not being calculated with 100% accuracy. Why is that?
Does that work in AKA Stoned Land? That is fine. Truth also works if false things are no longer out there. If you care about truth why don't you find a list of all the posts yoy made with errors so we can correct them with the latest and the greatest.
In this case, the truth is still a work in process. For the next step in the process - Maybe "yoy" and Noluchan's donkey can tell us why applying a linear calculation (d/v) to a non-linear velocity produces values for Time which are farther away from the Ballistic chart's value for T than rounding can explain?
So, Illustration A: Vb calculated from d/Tcalc, where Tcalc= (d=75ft)/Vel A: Please explain how, in the context of the highlighted range of interest on the concert field, Noluchan's idea to reconstruct Time by taking (d=75ft)/Vel[x+y] Feel free to consult Noluchan's Donkey, since it probably has better temperament and reading comprehension skills than either of you two have demonstrated.
If your Column c, Vel[x+y] (ft/s) represents an instantaneous velocity, it cannot be used in this manner. Make up your mind, does Column C represent instantaneous velocities, valid only at a single point, and not over any range?
Says the Donkey who managed to transform 0.86 seconds into 1.2119 seconds. Meanwhile... http://www.answers.com/Q /What_is_instantaneous_slope As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment.
http://www.answers.com/Q /What_is_instantaneous_slope As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment. To find what is at your source, we go to the link, which, like the link to the Khan Academy, only shows that you are bullshitting. You seem to have a special affinity in providing cut and paste bullshit as as some sort of profound knowledge. http://www.answers.com/Q/What_is_instantaneous_slope The instantaneous slope of a curve is the slope of that curve at a single point. In calculus, this is called the derivative. It also might be called the line tangent to the curve at a point. If you imagine an arbitrary curve (just any curve) with two points on it (point P and point Q), the slope between P and Q is the slope of the line connecting those two points. This is called a secant line. If you keep P where it is and slide Q closer and closer to P along the curve, the secant line will change slope as it gets smaller and smaller. When Q gets extremely close to P (so that there is an infinitesimal space between P and Q), then the slope of the secant line approximates the slope at P. When we take the limit of that tiny distance as it approaches zero (meaning we make the space disappear) we get the slope of the curve at P. This is the instantaneous slope or the derivative of the curve at P. Mathematically, we say that the slope at P = limh—>0 [f(x+h) - f(x)]÷h = df/dx, where h is the distance between P and Q, f(x) is the position of P, f(x+h) is the position of Q, and df/dx is the derivative of the curve with respect to x. The formula above is a specific case where the derivative is in terms of x and we're dealing with two dimensions. In physics, the instantaneous slope (derivative) of a position function is velocity, the derivative of velocity is acceleration, and the derivative of acceleration is jerk. Of course, the calculus formula P = limh—>0 [f(x+h) - f(x)]÷h = df/dx, where h is the distance between P and Q, f(x) is the position of P, f(x+h) is the position of Q, and df/dx is the derivative of the curve with respect to x was not used anywhere in your spreadsheet, so you are just bullshitting. Also, However, the slope of a bullet in flight is constantly changing, the deceleration is not constant, and the slope contains an infinite number of points. Moreover, you have merely bullshitted and have not described any formula to obtain the average velocity of the bullet over a given range, using instantaneous velocities. While you claim calculus formulas in your spreadsheet, you have yet to show a formula to sum changing parts of a spreadsheet column, i.e., sum row 1 and 2, sum row 1 thru 3, then row 1 thru 4, and so forth. I used such a formula and it showed that your column contained arithmetical errors not created by a spreadsheet formula. When you can program adding sums, I'll consider you doing calculus. As it is, you have not demostrated the ability to consistently add two numbers together, which is what you did to to sum that column. You added rows 1 and 2 to get the row 2 total; then you added row 3 to get the row 3 total, and so on, making two errors in 26 rows. You are fortunate it was now a thousand rows on a spreadsheet in a finance office. The formula for calculating average velocity (d/t) is given by the Khan Academy in the video you referenced. In their example, they divide a distance fo 1000m by 200s and get an average velocity of 5 m/s, and then they explicitly state, that siad result "doesn't necessarily equal the instantaneous velocities at particular points." The Khan Academy does not say that you can sum two instantaneous velocities and divide by two, and get an average velocity between the two points. See what you referenced. The first sentence is important — pretend you are a physics student. - [Instructor] Pretend you are a physics student. You are just getting out of class. You were walking home when you remembered that there was a Galaxy Wars marathon on tonight, so you'd do what every physics student would do: run. You're pretty motivated to get home, so say you start running at six meters per second. Maybe it's been a while since the last time you ran, so you have to slow down a little bit to two meters per second. When you get a little closer to home, you say: "No, Captain Antares wouldn't give up "and I'm not giving up either", and you start running at eight meters per second and you make it home just in time for the opening music. These numbers are values of the instantaneous speed. The instantaneous speed is the speed of an object at a particular moment in time. And if you include the direction with that speed, you get the instantaneous velocity. In other words, eight meters per second to the right was the instantaneously velocity of this person at that particular moment in time. Note that this is different from the average velocity. If your home was 1,000 meters away from school and it took you a total of 200 seconds to get there, your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip. In other words, let's say you jogged 60 meters in a time of 15 seconds. During this time you were speeding up and slowing down and changing your speed at every moment. Regardless of the speeding up or slowing down that took place during this path, your average velocity's still just gonna be four meters per second to the right; or, if you like, positive four meters per second. Just as your instantaneous velocity at two discrete and infinitesimal points can not be summed and divided by two to obtain average velocity, the instantaneous slope at two discrete and infinitesimal points will be different and cannot be used to calculate the slope of a traveling bullet whose velocity is contantly changing. While this bullshit about instantaneous slopes has diverted from your other bullshit about instantaneous velocities, you are still left searching to explain (1) your calculation used to derive average velocity over the specified distances, (2) your calculation used to change the formula for calculating average velocity over distance. Your chart stipulated distance and time. For 75 feet, you stipulated 0.02 seconds. This is your data, not mine. Using the formula, d/t=V(avg), that is 3,750 feet per second average velocity. If we assume that you meant the time to be anything between 0.015 and 0.025 seconds, that is 3000 - 5000 feet per second average velocity. For 1950 feet, you stipulated 0.86 seconds, and an average velocity of 2367.5926 feet per second, obtained by a formula you can neither present nor explain, nor can you provide any citation to any authority for your bullshit calculation. V(avg) = d/t = 1950/0.86 = 2267.4418 feet per second average velocity. If we assume that you meant the time to be anything between 0.855 and 0.865, then, V(avg) may equal 1950/0.0855 = 2280.7017 V(avg) may equal 1950/0.0865 = 2254.3353 Meanwhile, your bullshit 2367.5926 average velocity allows one to derive the time required to travel 1950 feet. 1950/2367.5926 = 0.823621429 seconds. Indeed, your second time for Tb, the time of the bullet, in your column E, reflects a bullet flight time of 0.823621 seconds, giving three less decimal points than I did, but rounding the the same precise thing at your chosen four decimal places, indicating how you derived that bullshit Tb from the bullshit average velocity. To check whether this bullshit time is not impossible with the stipulated data, one need only check if it is within the rounding possibilities of the stipulated data, i.e., from 0.855 to 0.865 seconds. Oh noes, your bullshit average velocity (0.823621) is not possible to reconcile with the stiplulated time, even allowing for the maximum rounding error. Your misbegotten time would round to 0.82 instead of 0.86. You have yet to explain how you can stipulate a bullet time of 0.86 seconds, and through the magic of VxH formulas, transform that time into 0.823621 seconds, and then use that visibly bullshit time to perform further bullshit calculations. If the bullet flew 1950 feet in 0.823621, why sure enough it went at an average velocity of 2367.5938 and covered 1950 feet. However, at the stipulated time of 0.86 seconds, at the bullshit average velocity of 2367.5938 feet per second, the bullet would have flown 2036.1307 feet. The stipulated distance is 1950 feet. At the maximum rounding down error to 0.855 seconds, at your bullshit average velocity of 2367.5926, the bullet would have flown 2024.292699 feet (0.855 x 2367.5926). The stipulated distance is 1950 feet. With your stipulated data, you may not have more or less than 1950 feet. You may not have less than 0.855 seconds flight time, nor more than 0.865 seconds flight time. You cannot change the distance the bullet flew, nor do more than consider a rounding error on the time. Your calculated numbers fail miserably. Your bullshit calculated numbers fall outside the maximum possible error attributable to a rounding error. Your bullshit calculations result in a new time, not within any rounding error, replacing 0.86 with 0.823621. Your bullshit average velocity over 1950 feet (2367.5926), at the maximum rounding error for stipulated time (0.86 rounded down to 0.855), requires the bullet to fly a minimum of 2024.292699 feet.
LOL. Idiot. ShooterCalculator.com Says: ======================== Professor DonkeyChan says: 1.2119 seconds nolu chan posted on 2017-10-30 19:58:41 ET https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53025&Disp=160#C160
Column B of above spreadsheet shows the specified distance and the specified time for that distance. Column C shows the specified time for the distance traveled. Column D shows the time rounded down to the minimum time possibly explained by rounding. Column E shows the time rounded up to the maximum time possibly explained by rounding. Column F shows the Average Velocity (d/t) calculated with the unadjusted time from Column C. Column G shows the Average Velocity (d/t) calculated with the minimum time possible from Column D. This minimum time of flight shows the maximum possible average velocity of the bullet. Column H shows the Average Velocity (d/t) calculsted with the maximum time possible from Column E. This maximum time of flight show the minimum average velocity of the bullet. Column I shows the time for sound to travel the distance at 1130 fps. Column J shows the time difference between the bullet and the sound using unadjusted time from Column C. Column K shows the maximum possible time difference between the bullet and the sound using the time rounded down in Column D. Column L shows the minimum possible time difference between the bullet and the sound using the time rounded up in Column E. Column N states VXH Average Velocity using undisclosed math, presumably of Klingon origin. Column O states the instantaneous velocities at the distances specified in Column B. These velocities reflect a specific and infinitesimal point it time only, and do not describe velocity at any other point in time. Comparing Columns H and N, Column H calculates the maximum possible average velocity with the time round down as far is is possible. Column N is the average velocity claimed by VxH, using his secret Klingon mathematics. Notice his secret method obtain an average velocity well below the maximum possible for 75 feet, but comes nearer to the maximum possible with every calculation, and at 1200 feet his calculations leave the realm of the possible. At 1200 feet, at the specified time of 0.46 seconds, the average velocity would be 2608.70 feet per second (1200/0.46). Anyone can do the arithmetic. At 1200 feet, at 0.46 seconds rounded down as far as possible to 0.455 seconds (Column D), the maximum average veocity of 2637.36 feet per second (Column G) is achieved (2637.36/0.455). Anyone can still do the arithmetic. At this point, the VxH calculations exceed the possibilities of reality and achieve 2675.1176 feet per second. After this point, every VxH calculation widens the error. At 1950 feet, the Column G max average velocity is 2280.70 (1950/0.0855). After more calculations, the VxH error expands the difference to 2367.5926 feet per second. If carried on to further distances, the error will simply keep increasing. He started with 64% of the maximum possible average velocity, and surpassed 100% of the maximum on his 16th calculation, and continued to surpass the maximum possible average velocity by a greater and greater amount. Moreover, the distance and the time were a given.
...ft........ sec .... sec per VxH
75 0.02 0.023427
150 0.05 0.047413
225 0.07 0.071971
300 0.10 0.097113
375 0.12 0.122843
450 0.15 0.149183
525 0.18 0.176138
600 0.20 0.203720
675 0.23 0.231943
750 0.26 0.260820
825 0.29 0.290357
900 0.32 0.320574
975 0.36 0.351496
1050 0.39 0.383128
1125 0.42 0.415484
1200 0.46 0.448578
1275 0.49 0.482427
1350 0.53 0.517054
1425 0.56 0.552465
1500 0.60 0.588675
1575 0.64 0.625711
1650 0.68 0.663578
1725 0.73 0.702290
1800 0.77 0.741864
1875 0.81 0.782303
1950 0.86 0.082621
Notice how VxH, in his calculations, at and after 1200 feet, reduces the time of flight of the bullet by more than any possible amount of rounding from two decimal places. By 1950 feet, VxH has "rounded off" 0.86 and amazingly reduced the stated flight time to his own preferred 0.82621.
>>By 1950 feet, VxH has "rounded off" 0.86 Nope. Not a rounding error Super Genius. It's an artifact manufacted from the AVERAGING curve. >>preferred 0.82621. Nope. Try to keep up - - I've moved on with a revised curve that reconstructs time from Velocity and Distance, As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment. So, Professor DonkeyChan -- Here is the ballistic data table generated for 1 yard intervals from 1875 to 1950 ft. Drag Function: G1 Wind Speed: 0 mph Corrected For Atmosphere
You have explored methods which require require rewriting the bullet flight times far beyond any possible rounding error. Reconstructing the given travel time is VxH BULLSHIT. Time and distance are given. Rounding the given time up or down does not help your bullshit work. Your bullshit methodology changes the given 0.86 seconds elapsed time to 0.82 seconds. There is no valid formula in the world for that. Time and distance are given data. Average velocity equals distance divided by time. Distance in feet, divideded by time in seconds, yields velocity in feet per second. Column B of above spreadsheet shows the specified distance and the specified time for that distance. Column C shows the specified time for the distance traveled. Column D shows the time rounded down to the minimum time possibly explained by rounding. Column E shows the time rounded up to the maximum time possibly explained by rounding. Column F shows the Average Velocity (d/t) calculated with the unadjusted time from Column C. Column G shows the Average Velocity (d/t) calculated with the minimum time possible from Column D. This minimum time of flight shows the maximum possible average velocity of the bullet. Column H shows the Average Velocity (d/t) calculsted with the maximum time possible from Column E. This maximum time of flight show the minimum average velocity of the bullet. Column I shows the time for sound to travel the distance at 1130 fps. Column J shows the time difference between the bullet and the sound using unadjusted time from Column C. Column K shows the maximum possible time difference between the bullet and the sound using the time rounded down in Column D. Column L shows the minimum possible time difference between the bullet and the sound using the time rounded up in Column E. Column N states VXH Average Velocity using undisclosed math, presumably of Klingon origin. Column O states the instantaneous velocities at the distances specified in Column B. There velocities reflect a specific and infinitesimal point it time only, and do not describe velocity at any other point in time. Comparing Columns H and N, Column H calculates the maximum possible average velocity with the time round down as far is is possible. Column N is the average velocity claimed by VxH, using his secret Klingon mathematics. Notice his secret method obtain an average velocity well below the maximum possible for 75 feet, but comes nearer to the maximum possible with every calculation, and at 1200 feet his calculations leave the realm of the possible. At 1200 feet, at the specified time of 0.46 seconds, the average velocity would be 2608.70 feet per second (1200/0.46). Anyone can do the arithmetic. At 1200 feet, at 0.46 seconds rounded down as far as possible to 0.455 seconds (Column D), the maximum average veocity of 2637.36 feet per second (Column G) is achieved (2637.36/0.455). Anyone can still do the arithmetic. At this point, the VxH calculations exceed the possibilities of reality and achieve 2675.1176 feet per second. After this point, every VxH calculation widens the error. At 1950 feet, the Column G max average velocity is 2280.70 (1950/0.0855). After more calculations, the VxH error expands the difference to 2367.5926 feet per second. If carried on to further distances, the error will simply keep increasing. He started with 64% of the maximum possible average velocity, and surpassed 100% of the maximum on his 16th calculation, and continued to surpass the maximum possible average velocity by a greater and greater amount. Moreover, the distance and the time were a given.
ft.......... sec..... sec
75 0.02 0.023427
150 0.05 0.047413
225 0.07 0.071971
300 0.10 0.097113
375 0.12 0.122843
450 0.15 0.149183
525 0.18 0.176138
600 0.20 0.203720
675 0.23 0.231943
750 0.26 0.260820
825 0.29 0.290357
900 0.32 0.320574
975 0.36 0.351496
1050 0.39 0.383128
1125 0.42 0.415484
1200 0.46 0.448578
1275 0.49 0.482427
1350 0.53 0.517054
1425 0.56 0.552465
1500 0.60 0.588675
1575 0.64 0.625711
1650 0.68 0.663578
1725 0.73 0.702290
1800 0.77 0.741864
1875 0.81 0.782303
1950 0.86 0.082621
Notice how VxH, in his calculations, at and after 1200 feet, reduces the time of flight of the bullet by more than any possible amount of rounding from two decimal places. By 1950 feet, VxH has "rounded off" 0.86 and amazingly calculated, by secret methodology, the stated flight time to his own preferred 0.82621. That is VxH bullshit. Not only wrong but impossible on its face. Now tell us, Professor DonkeyChan - from the data provided, what is the average Velocity for the 75 ft segment ending at 1950 ft (1950ft, being the point at which, BTW, the instantaneous velocity is 1609fps)? The average velocity of any object covering 1950 feet in 0.86 seconds is 1950/0.86 = 2267.4419 feet per second. It could be a flying refrigerator. If it goes 1950 feet in 0.86 seconds, the average velocity is 2267.4419 seconds. The object could have sped up and slowed down between 0 and 1950 feet in any manner and it makes no difference. If the object covers the 1950 feet in 0.86 seconds, the average velocity for the 1950 foot distance is 2267.4419 seconds. Recall the Khan Academy video you previously referenced: - [Instructor] Pretend you are a physics student. You are just getting out of class. You were walking home when you remembered that there was a Galaxy Wars marathon on tonight, so you'd do what every physics student would do: run. You're pretty motivated to get home, so say you start running at six meters per second. Maybe it's been a while since the last time you ran, so you have to slow down a little bit to two meters per second. When you get a little closer to home, you say: "No, Captain Antares wouldn't give up "and I'm not giving up either", and you start running at eight meters per second and you make it home just in time for the opening music. These numbers are values of the instantaneous speed. The instantaneous speed is the speed of an object at a particular moment in time. And if you include the direction with that speed, you get the instantaneous velocity. In other words, eight meters per second to the right was the instantaneously velocity of this person at that particular moment in time. Note that this is different from the average velocity. If your home was 1,000 meters away from school and it took you a total of 200 seconds to get there, your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip. In other words, let's say you jogged 60 meters in a time of 15 seconds. During this time you were speeding up and slowing down and changing your speed at every moment. Regardless of the speeding up or slowing down that took place during this path, your average velocity's still just gonna be four meters per second to the right; or, if you like, positive four meters per second. [snip] The instantaneous velocity at 1950 feet is irrelevant to the calculation of the average velocity over the range 0 to 1950 feet.
LOL. It's not a rounding error Professor DonkeyChan. How you coming along with that Average Velocity for the 75 foot segment ending at 1950 ft?
It came along quite well. Anything that travels 1950 feet in 1.06 seconds travels an average velocity of 2122.64 feet per second. The formula is distance divided by time. How are you coming along with your bullet going splat at ~520 feet ground distance from Mandalay Bay? How did you work out that negative 33º angle? Side a represents the vertical height of Paddock's vantage point. At the 32nd floor, and at 10.9 feet per floor, (32-1) x 10.9 = 338 feet. The VxH specified shooting angle was -33°. This should probably be expressed as a positive angle of declination. Not all ballistic calculators will even accept a negative angle value, but specify 0 to 90 degrees. For another calculator, see: http://gundata.org/blog/post/223-ballistics-chart/ It appears that VxH drew an imaginary horizontal line d at a vertical height of 338 feet from the ground, and an imaginary 338 foot line e down to the ground, bringing into view a rectangle with a mirror image triangle to that above. VxH guessed 33º as the acute angle formed at the junction of sides c and imaginary side d at point B. VxH guessed very wrongly. With a specified shooting angle of 33º at the junction of lines c and d, the angle made by sides c and b would also be 33º, and angle ß, made by sides a and c would be 57º. (The right angle at point A is 90º. The other two angles must add up to 90º.) With side a being 338 feet, side b would be 520.4743578 feet, and side c would be 620.5944 feet. As may be seen, disregarding gravity, if the bullet flew downward at the specified 33º from a height of 338 feet, it would fly a straight line of sight path into the ground at ~520 feet from the Mandalay Bay at ground level. Calculating the bullet velocity after that point may be difficult, even with secret Klingon math.
BZZZT! Probably not, since using 0.33 instead of -0.33 produces a slower velocity: (0.33) 1950 0.89 1489 (-0.33) 1950 0.86 1609
#143. To: VxH, A K A Stone (#141)
BZZZT! Probably not, since using 0.33 instead of -0.33 produces a slower velocity: There is no 33 degree angle involved. Using your trajectory, Paddock would have come closer to shooting off his big toe than hitting anywhere in the festival venue. Learn to read: Declination is downward. Negative 33 degrees inclination is the same as 33 degrees declination. It is the difference between your preferred -33 degrees upward and 33 degrees downward. 33 degrees downward points down. Negative 33 degrees downward points up. It is like walking negative 33 feet east is walking 33 feet west. For another calculator, see: The gundata entry specifies "Shooting angle (0..89)." Stick a negative value in there and it will reject. As there is no such thing as a triangle with negative angles, the values for every angle of a triangle are positive values. In a triangle with sides -3 and -4, a2 + b2 = c2 would yield a hypotenuse of positive 5. (0.33) 1950 0.89 1489 (-0.33) 1950 0.86 1609 The data available at the links shows the only data change between my two charts is one is -33 and the other is 33. Not so for the chart you just created with yet another time calculation. You changed the input data. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=75dcb734 -33 degrees http://www.shooterscalculator.com/images/trajectory/ballistic_trajectory_chart_75dcb734.png This chart made with the original -33 data, shows the bullet rise above the original altitude, and remain above that altitude, for over 300 yards. This is an amazing feat for a bullet shot on a steep downward angle. - - - - - - - - - - http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=fd15e1b9 33 degrees http://www.shooterscalculator.com/images/trajectory/ballistic_trajectory_chart_fd15e1b9.png Amazingly, when the angle is changed from -33 to 33, the flight path does not change, according to your calculator. - - - - - - - - - - When your calculator permits you to enter ridiculous data, it provides you with ridiculous results. As one may observe, it provides the precise same flight trajectory, whether at 33 or -33. When fired at 33 degrees downward, the bullet goes upward and remains above the original location for over 300 yards. The data available at the links shows the only data change to be -33 to 33. The time for 650 yards/1950 feet is 0.86 in either instance. The average velocity for any object that travels 1950 feet in 0.86 seconds is 1950/0.86 = 2267.4418 ft/sec. - - - - - - - - - - YOUR DATA WITH A NEW TIME SHOWS YOU ALTERED THE INPUT DATA. And your flight trajectory chart for -33 degrees featuring a new time http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=81e7edd6 http://www.shooterscalculator.com/images/trajectory/ballistic_trajectory_chart_81e7edd6.png Notice that with the projectile purported fired at a 33 degree downward angle, the projectile maintains its original altitude for about 150 yards. Of course, in your derivation of data, you changed the properties of the chart: Drag Function: G1 Corrected For Atmosphere - - - - - - - - - - - - - - - - - - - - To see the prior input data, just look: As for your magic ability to fire rounds down at 33º, and have them either rise or maintain altitude for hundreds of yards,
Top • Page Up • Full Thread • Page Down • Bottom/Latest
#73. To: A K A Stone, VXH, buckeroo, tooconservative, cz82, redleghunter, sneakypete, Pinguinite, Vicomte13, Liberator, Deckard (#1)
Found this interesting video.
Thread: 308 Ammo Help
This is a .223 ballistics chart (external) generated using our ballistic trajectory calculator. Based off a standard 55gr bullet leaving the barrel at 3,215fps and follows the bullet trajectory all the way to 1000 yards in steps of 50 yard increments. The charting shows the range, drop (based off a 1.5" scope mount), current velocity, energy, and time in seconds in relation to the bullets movement through space and time. This chart does not account for atmospheric conditions, so if you want to take in to effect these things check out the calculators official page. The Ballistic Coefficient for the .223 Remington, Remington Metal Case, 55gr is 0.202 (in this example) but, but may also range from .185 bc to .257
-31.7981 [drop, inches]
1588 [Velocity]
308 [energy]
532 [time, milliseconds]
#78. To: nolu chan (#73)
#81. To: VxH (#78)
All numbers he pulled out of his arse?
#82. To: nolu chan (#81)
(Edited)
The audio he used is presented.
#83. To: VxH (#82)
The amplitude graphs of the audio referenced on my meme can be reproduced by anyone with minimal tools. It's REPRODUCIBLE - that's what differentiates valid science from conspiratorial buffoonery.
#86. To: nolu chan (#83)
That you reproduce meaningless bullshit is meaningful
#88. To: VxH (#86)
The amplitude graphs are reproducible...
#89. To: nolu chan (#88)
#90. To: VxH (#89)
Maybe you just don't have what it takes.
#91. To: nolu chan (#90)
(Edited)
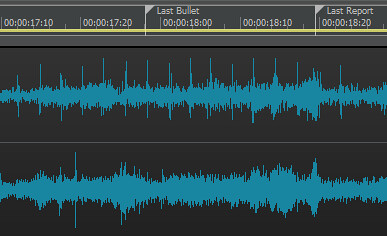

#92. To: VxH (#91)
Now, ask your donkey - what distance does that MEASURED absolute time difference correspond to on the chart?
Bullet Time, Velocity FPS, Tb–Ts
Tb = Time of bullet
Ts = Time of sound, 1.062 seconds @ 1,130 feet per second (FPS) (72ºF, 20% Humidity)
Ts – Tb = Time difference between Tb and Ts
Column 2 = Tb stepped in 100 FPS increments, beginning with Ts
Column 3 = Ts – Tb (time in seconds supersonic bullet arrives ahead of sound) Bullet time (s), Bullet average velocity (FPS), time difference to sound at 1,200 feet (s)
Bullet time (s) Bullet average vel FPS Time diff Ts-Tb 1.062 1130 0.000 0.976 1230 0.086 0.902 1330 0.160 0.839 1430 0.223 0.784 1530 0.278 0.736 1630 0.326 0.694 1730 0.368 0.656 1830 0.406 0.622 1930 0.440 0.591 2030 0.471 0.563 2130 0.499 0.538 2230 0.524 0.515 2330 0.547 0.494 2430 0.568 0.474 2530 0.588 0.456 2630 0.606 0.440 2730 0.622 0.424 2830 0.638 0.410 2930 0.652 0.396 3030 0.666 0.383 3130 0.679 0.372 3230 0.690 0.360 3330 0.702 0.350 3430 0.712 0.340 3530 0.722 0.331 3630 0.731 0.322 3730 0.740 0.313 3830 0.749 0.305 3930 0.757 0.298 4030 0.764
#93. To: nolu chan (#92)
(Edited)

#95. To: VxH (#93)
Since we KNOW from the observed audio Vb is supersonic, we can treat the difference between Tb and Ts as Absolute.
#96. To: nolu chan (#95)
(Edited)
They have a spreadsheet function for that.


#97. To: VxH (#96)

#99. To: nolu chan (#97)
(Edited)
Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fpsRange Time Vel[x+y] (ft) (s) (ft/s) 0 0.00 3240 75 0.02 3163 150 0.05 3088 225 0.07 3014 300 0.10 2941 375 0.12 2870 450 0.15 2799 525 0.18 2730 600 0.20 2662 675 0.23 2595 750 0.26 2529 825 0.29 2465 900 0.32 2401 975 0.36 2337 1050 0.39 2275 1125 0.42 2214 1200 0.46 2154 1275 0.49 2095 1350 0.53 2036 1425 0.56 1979 1500 0.60 1923 1575 0.64 1867 1650 0.68 1813 1725 0.73 1760 1800 0.77 1708 1875 0.81 1658 1950 0.86 1609 2025 0.91 1561 2100 0.96 1515 2175 1.01 1470 2250 1.06 1426 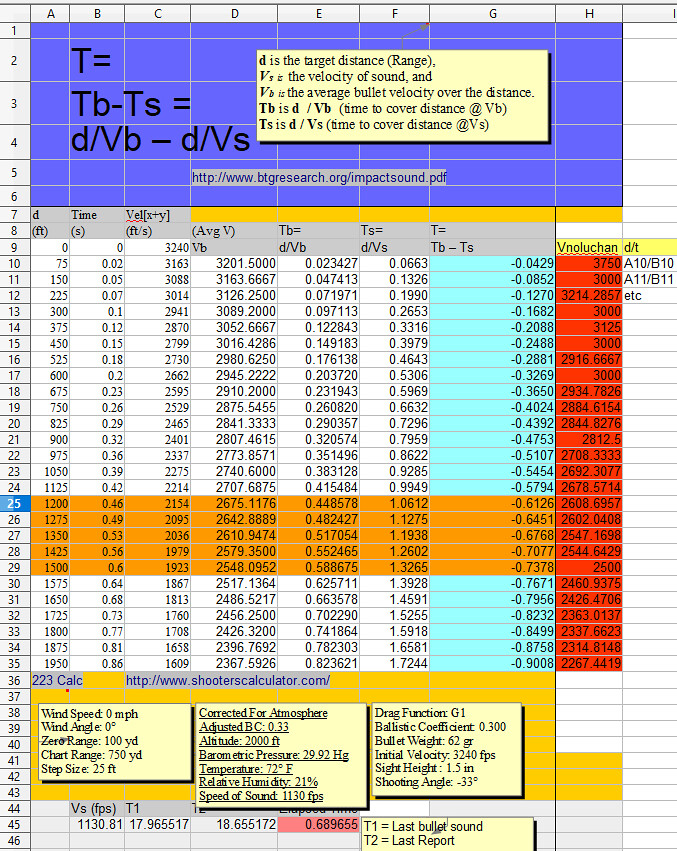

#101. To: VxH, A K A Stone (#99)
and the data was directly entered into the cells by hand.
I found/took their formula, built a spreadsheet, and plugged in 223 balistic data generated via shooterscalculator.com:
#102. To: nolu chan (#101)
(Edited)
=SUM(C$9:C11)/L10
=SUM(C$9:C12)/L11
etc.
Where column L contains 1 @ row 8 and =+L8+1, =+L9+1 etc for rows 9..34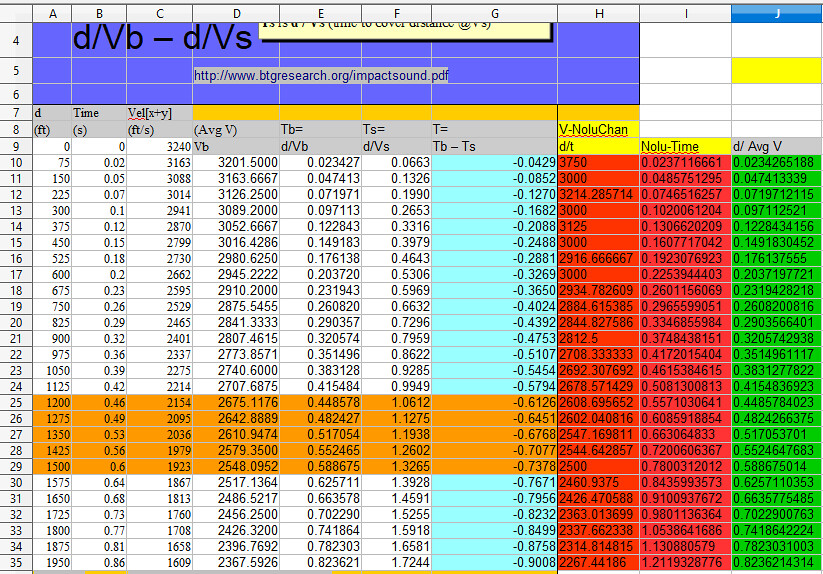
#103. To: VxH (#102)
#106. To: A K A Stone (#103)
Chan is kicking your ass and you are looking foolish with all your errors.
#107. To: VxH (#106)
#108. To: A K A Stone (#107)
(Edited)
A: { crickets crickets crickets }
#109. To: VxH (#108)
#115. To: A K A Stone (#109)
#116. To: VxH (#115)
(Edited)
Truth is great and will prevail unless deprived of her natural weapons, free argument and debate.
#117. To: A K A Stone (#116)
(Edited)
If you care about truth why don't you find a list of all the posts yoy made with errors
#119. To: A K A Stone, noluchan, buckeroo (#117)
(Edited)
{ crickets crickets crickets }
Illustration B: Vb using my original Average of summed Velocity values. B:
B:
does not seem to produce results that magically render the values produced by summing and averaging Vel[x+y] into "bullshit"?
#128. To: VxH, A K A Stone (#119)
Illustration A: Vb calculated from d/Tcalc, where Tcalc= (d=75ft)/Vel
#129. To: nolu chan (#128)
(Edited)
it cannot be used in this manner.
#130. To: VxH, A K A Stone (#129)
Meanwhile...
Answer byBlue
Confidence votes 38.3K When Q gets extremely close to P (so that there is an infinitesimal space between P and Q), then the slope of the secant line approximates the slope at P. When we take the limit of that tiny distance as it approaches zero (meaning we make the space disappear) we get the slope of the curve at P. This is the instantaneous slope or the derivative of the curve at P.
Video transcript
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
#131. To: nolu chan (#130)

Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%1950 0.86 1609 4 d Time (avg) Vel[x+y] 5 (ft) d/Vel[x+y] (ft/s) 32 1950 1.2119 1609
#132. To: VxH, A K A Stone (#131)
Unresponsive obfuscatory yukonesque bullshit
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
Distance and time specified Time rounded to plus or minus maximum Avg velocity Avg velocity Avg velocity time for sound ABS Tb - Ts ABS Tb - Ts ABS Tb - Ts time as given max possible min possible to travel dist time as given max possible min possible B C D E F G H I J K L N O P d Time Time -.005 Time +.005 Avg Vel unadj Avg Vel max Avg Vel min t for sound ABS Tdiff unadj ABS Tdiff MAX ABS Tdiff MIN VxH Avg Vel VxH Instant VxH Tdiff (ft) (seconds) (seconds) b/c b/d b/e b/1130 ABS(c8-i8) ABS(d8-i8) ABS(E8-I8) Velocity Tb-Ts 7 0 0.00 3240 8 75 0.02 0.015 0.025 3750.00 5000.00 3000.0000 0.0664 0.0464 0.0514 0.0414 3201.5000 3163 0.0429 9 150 0.05 0.045 0.055 3000.00 3333.33 2727.2727 0.1327 0.0827 0.0877 0.0777 3163.6667 3088 0.0852 10 225 0.07 0.065 0.075 3214.29 3461.54 3000.0000 0.1991 0.1291 0.1341 0.1241 3126.2500 3014 0.1270 11 300 0.10 0.095 0.105 3000.00 3157.89 2857.1429 0.2655 0.1655 0.1705 0.1605 3089.2000 2941 0.1682 12 375 0.12 0.115 0.125 3125.00 3260.87 3000.0000 0.3319 0.2119 0.2169 0.2069 3052.6667 2870 0.2088 13 450 0.15 0.145 0.155 3000.00 3103.45 2903.2258 0.3982 0.2482 0.2532 0.2432 3016.4286 2799 0.2488 14 525 0.18 0.175 0.185 2916.67 3000.00 2837.8378 0.4646 0.2846 0.2896 0.2796 2980.6250 2730 0.2881 15 600 0.20 0.195 0.205 3000.00 3076.92 2926.8293 0.5310 0.3310 0.3360 0.3260 2945.2222 2662 0.3269 16 675 0.23 0.225 0.235 2934.78 3000.00 2872.3404 0.5973 0.3673 0.3723 0.3623 2910.2000 2595 0.3650 17 750 0.26 0.255 0.265 2884.62 2941.18 2830.1887 0.6637 0.4037 0.4087 0.3987 2875.5455 2529 0.4024 18 825 0.29 0.285 0.295 2844.83 2894.74 2796.6102 0.7301 0.4401 0.4451 0.4351 2841.3333 2465 0.4392 19 900 0.32 0.315 0.325 2812.50 2857.14 2769.2308 0.7965 0.4765 0.4815 0.4715 2807.4615 2401 0.4753 20 975 0.36 0.355 0.365 2708.33 2746.48 2671.2329 0.8628 0.5028 0.5078 0.4978 2773.8571 2337 0.5107 21 1050 0.39 0.385 0.395 2692.31 2727.27 2658.2278 0.9292 0.5392 0.5442 0.5342 2740.6000 2275 0.5454 22 1125 0.42 0.415 0.425 2678.57 2710.84 2647.0588 0.9956 0.5756 0.5806 0.5706 2707.6875 2214 0.5794 23 1200 0.46 0.455 0.465 2608.70 2637.36 2580.6452 1.0619 0.6019 0.6069 0.5969 2675.1176 2154 0.6260 24 1275 0.49 0.485 0.495 2602.04 2628.87 2575.7576 1.1283 0.6383 0.6433 0.6333 2642.8889 2095 0.6451 25 1350 0.53 0.525 0.535 2547.17 2571.43 2523.3645 1.1947 0.6647 0.6697 0.6597 2610.9474 2036 0.6768 26 1425 0.56 0.555 0.565 2544.64 2567.57 2522.1239 1.2611 0.7011 0.7061 0.6961 2579.3500 1979 0.7077 27 1500 0.60 0.595 0.605 2500.00 2521.01 2479.3388 1.3274 0.7274 0.7324 0.7224 2548.0952 1923 0.7378 28 1575 0.64 0.635 0.645 2460.94 2480.31 2441.8605 1.3938 0.7538 0.7588 0.7488 2517.1364 1867 0.7671 29 1650 0.68 0.675 0.685 2426.47 2444.44 2408.7591 1.4602 0.7802 0.7852 0.7752 2486.5217 1813 0.7956 30 1725 0.73 0.725 0.735 2363.01 2379.31 2346.9388 1.5265 0.7965 0.8015 0.7915 2456.2500 1760 0.8232 31 1800 0.77 0.765 0.775 2337.66 2352.94 2322.5806 1.5929 0.8229 0.8279 0.8179 2426.3200 1708 0.8499 32 1875 0.81 0.805 0.815 2314.81 2329.19 2300.6135 1.6593 0.8493 0.8543 0.8443 2395.7692 1658 0.8758 33 1950 0.86 0.855 0.865 2267.44 2280.70 2254.3353 1.7257 0.8657 0.8707 0.8607 2367.5926 1609 0.9008 34 2025 0.91 0.905 0.915 2225.27 2237.57 2213.1148 1.7920 0.8820 0.8870 0.8770 35 2100 0.96 0.955 0.965 2187.50 2198.95 2176.1658 1.8584 0.8984 0.9034 0.8934 36 2175 1.01 1.005 1.015 2153.47 2164.18 2142.8571 1.9248 0.9148 0.9198 0.9098 37 2250 1.06 1.055 1.065 2122.64 2132.70 2112.6761 1.9912 0.9312 0.9362 0.9262
....d ........ t ... Vxh
#133. To: nolu chan (#132)
(Edited)

Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 1000 yd
Maximum Range: 50002 yd
Step Size: 1 yd
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fps Range Time Vel[x+y] (ft) (s) (ft/s) 1875 0.81 1658 1878 0.81 1656 1881 0.82 1654 1884 0.82 1652 1887 0.82 1650 1890 0.82 1648 1893 0.82 1646 1896 0.83 1644 1899 0.83 1642 1902 0.83 1640 1905 0.83 1638 1908 0.83 1636 1911 0.83 1634 1914 0.84 1632 1917 0.84 1630 1920 0.84 1628 1923 0.84 1626 1926 0.84 1624 1929 0.85 1622 1932 0.85 1621 1935 0.85 1619 1938 0.85 1617 1941 0.85 1615 1944 0.86 1613 1947 0.86 1611 1950 0.86 1609
Now tell us, Professor DonkeyChan - from the data provided, what is the average Velocity for the 75 ft segment ending at 1950 ft (1950ft, being the point at which, BTW, the instantaneous velocity is 1609fps)?
#137. To: VxH (#133)
[VxH #133] Nope. Try to keep up - - I've moved on with a revised curve that reconstructs time from Velocity and Distance,
YOUR CALCULATED DATA IS ALL BULLSHIT, AS ARE YOU
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
Distance and time specified Time rounded to plus or minus maximum Avg velocity Avg velocity Avg velocity time for sound ABS Tb - Ts ABS Tb - Ts ABS Tb - Ts time as given max possible min possible to travel dist time as given max possible min possible B C D E F G H I J K L N O P d Time Time -.005 Time +.005 Avg Vel unadj Avg Vel max Avg Vel min t for sound ABS Tdiff unadj ABS Tdiff MAX ABS Tdiff MIN VxH Avg Vel VxH Instant VxH Tdiff (ft) (seconds) (seconds) b/c b/d b/e b/1130 ABS(c8-i8) ABS(d8-i8) ABS(E8-I8) Velocity Tb-Ts 7 0 0.00 3240 8 75 0.02 0.015 0.025 3750.00 5000.00 3000.0000 0.0664 0.0464 0.0514 0.0414 3201.5000 3163 0.0429 9 150 0.05 0.045 0.055 3000.00 3333.33 2727.2727 0.1327 0.0827 0.0877 0.0777 3163.6667 3088 0.0852 10 225 0.07 0.065 0.075 3214.29 3461.54 3000.0000 0.1991 0.1291 0.1341 0.1241 3126.2500 3014 0.1270 11 300 0.10 0.095 0.105 3000.00 3157.89 2857.1429 0.2655 0.1655 0.1705 0.1605 3089.2000 2941 0.1682 12 375 0.12 0.115 0.125 3125.00 3260.87 3000.0000 0.3319 0.2119 0.2169 0.2069 3052.6667 2870 0.2088 13 450 0.15 0.145 0.155 3000.00 3103.45 2903.2258 0.3982 0.2482 0.2532 0.2432 3016.4286 2799 0.2488 14 525 0.18 0.175 0.185 2916.67 3000.00 2837.8378 0.4646 0.2846 0.2896 0.2796 2980.6250 2730 0.2881 15 600 0.20 0.195 0.205 3000.00 3076.92 2926.8293 0.5310 0.3310 0.3360 0.3260 2945.2222 2662 0.3269 16 675 0.23 0.225 0.235 2934.78 3000.00 2872.3404 0.5973 0.3673 0.3723 0.3623 2910.2000 2595 0.3650 17 750 0.26 0.255 0.265 2884.62 2941.18 2830.1887 0.6637 0.4037 0.4087 0.3987 2875.5455 2529 0.4024 18 825 0.29 0.285 0.295 2844.83 2894.74 2796.6102 0.7301 0.4401 0.4451 0.4351 2841.3333 2465 0.4392 19 900 0.32 0.315 0.325 2812.50 2857.14 2769.2308 0.7965 0.4765 0.4815 0.4715 2807.4615 2401 0.4753 20 975 0.36 0.355 0.365 2708.33 2746.48 2671.2329 0.8628 0.5028 0.5078 0.4978 2773.8571 2337 0.5107 21 1050 0.39 0.385 0.395 2692.31 2727.27 2658.2278 0.9292 0.5392 0.5442 0.5342 2740.6000 2275 0.5454 22 1125 0.42 0.415 0.425 2678.57 2710.84 2647.0588 0.9956 0.5756 0.5806 0.5706 2707.6875 2214 0.5794 23 1200 0.46 0.455 0.465 2608.70 2637.36 2580.6452 1.0619 0.6019 0.6069 0.5969 2675.1176 2154 0.6260 24 1275 0.49 0.485 0.495 2602.04 2628.87 2575.7576 1.1283 0.6383 0.6433 0.6333 2642.8889 2095 0.6451 25 1350 0.53 0.525 0.535 2547.17 2571.43 2523.3645 1.1947 0.6647 0.6697 0.6597 2610.9474 2036 0.6768 26 1425 0.56 0.555 0.565 2544.64 2567.57 2522.1239 1.2611 0.7011 0.7061 0.6961 2579.3500 1979 0.7077 27 1500 0.60 0.595 0.605 2500.00 2521.01 2479.3388 1.3274 0.7274 0.7324 0.7224 2548.0952 1923 0.7378 28 1575 0.64 0.635 0.645 2460.94 2480.31 2441.8605 1.3938 0.7538 0.7588 0.7488 2517.1364 1867 0.7671 29 1650 0.68 0.675 0.685 2426.47 2444.44 2408.7591 1.4602 0.7802 0.7852 0.7752 2486.5217 1813 0.7956 30 1725 0.73 0.725 0.735 2363.01 2379.31 2346.9388 1.5265 0.7965 0.8015 0.7915 2456.2500 1760 0.8232 31 1800 0.77 0.765 0.775 2337.66 2352.94 2322.5806 1.5929 0.8229 0.8279 0.8179 2426.3200 1708 0.8499 32 1875 0.81 0.805 0.815 2314.81 2329.19 2300.6135 1.6593 0.8493 0.8543 0.8443 2395.7692 1658 0.8758 33 1950 0.86 0.855 0.865 2267.44 2280.70 2254.3353 1.7257 0.8657 0.8707 0.8607 2367.5926 1609 0.9008 34 2025 0.91 0.905 0.915 2225.27 2237.57 2213.1148 1.7920 0.8820 0.8870 0.8770 35 2100 0.96 0.955 0.965 2187.50 2198.95 2176.1658 1.8584 0.8984 0.9034 0.8934 36 2175 1.01 1.005 1.015 2153.47 2164.18 2142.8571 1.9248 0.9148 0.9198 0.9098 37 2250 1.06 1.055 1.065 2122.64 2132.70 2112.6761 1.9912 0.9312 0.9362 0.9262
d ........ given..........Vxh bullshit
[VxH]
1950 0.86 1609
Video transcript
#138. To: nolu chan (#137)
beyond any possible rounding error
#139. To: VxH, A K A Stone (#138)
How you coming along with that Average Velocity for the 75 foot segment ending at 1950 ft?
#141. To: nolu chan (#139)
This should probably be expressed as a positive angle of declination.
Replies to Comment # 141. This should probably be expressed as a positive angle of declination.
The VxH specified shooting angle was -33°. This should probably be expressed as a positive angle of declination. Not all ballistic calculators will even accept a negative angle value, but specify 0 to 90 degrees.
BZZZT! Probably not, since using 0.33 instead of -0.33 produces a slower velocity:
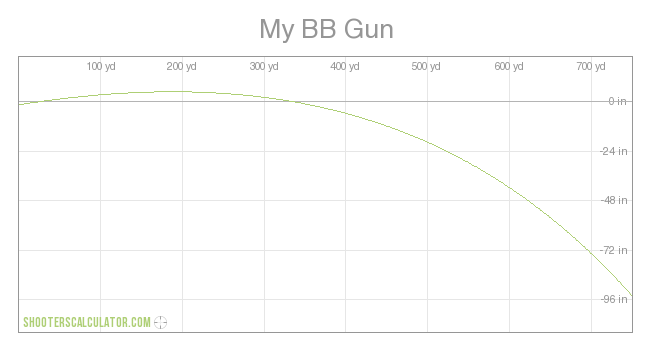
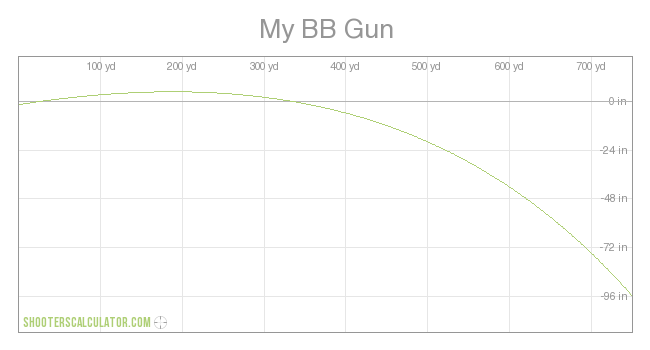
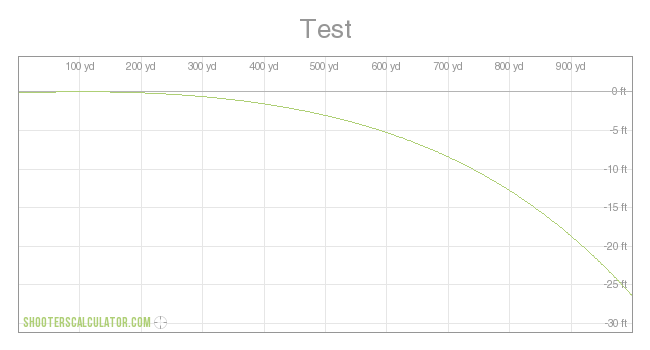
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°
Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd [Was 25 yd/75 feet]
Chart Range: 1000 yd[Was 750 yd]
Maximum Range: 50002 yd [Was 750 yd/2250 ft]
Step Size: 1 yd [Was 25 yd/75 ft]
Adjusted BC: 0.307 [was 0.300]
Altitude: 0 ft [was 2000 ft]
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fps 
End Trace Mode for Comment # 141.
[Home] [Headlines] [Latest Articles] [Latest Comments] [Post] [Mail] [Sign-in] [Setup] [Help] [Register]
