United States News
See other United States News Articles
Title: Forensic acoustic proof of SECOND shooter in the Las Vegas massacre
Source:
[None]
URL Source: https://www.youtube.com/watch?v=JxmEFeKy8aI
Published: Oct 11, 2017
Author: Mike Adams TheHealthRanger
Post Date: 2017-10-11 00:40:47 by A K A Stone
Keywords: None
Views: 58762
Comments: 148
Post Comment Private Reply Ignore Thread
Top • Page Up • Full Thread • Page Down • Bottom/Latest
Comments (1-89) not displayed.
.
.
.
#90. To: VxH (#89)
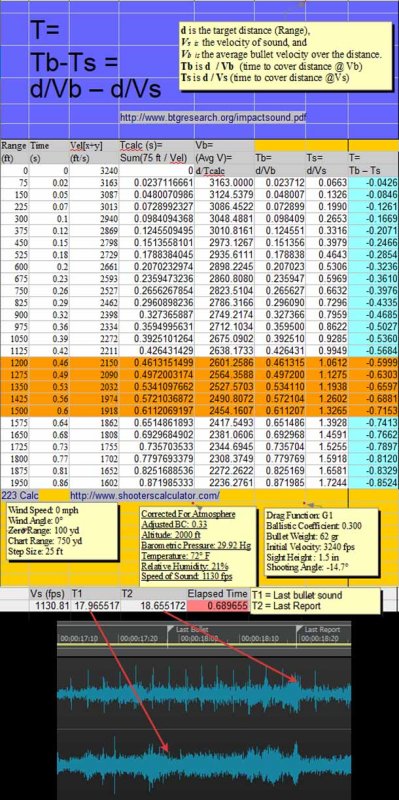
On your spreadsheet chartoon, notice that you calculate T = Tb - Ts. You calculate elapsed time as the time it took the bullet to travel, minus the time it took the sound to travel. As the bullet is supersonic, and sound is a constant, the sound would travel 400 yards in 1.06s and the bullet would travel the 400 yards in less than 1.06s. Subtracting 1.06 from a smaller number will always yield a negative number. At 1200 feet, you actually calculate Tb as 0.448578s, and Ts as 1.062s and calculate the T as -0.6126, negative 0.6126 seconds. The average donkey could recognize that something is wrong when the result is negative time. Just what do you think happens in negative 0.6126 seconds? You could at least recognize that if you get a negative number, you have stated the required formula backwards, and you proceeded to perform the calculation backwards, and present the bass ackwards result of your understanding of the study you looked at. You've got what it takes to make bullets travel in negative time. Your brain apparently has zero amplitude.
>>at 1200 feet, you actually calculate Tb as 0.448578s, and Ts as 1.062s and calculate the T as -0.6126, negative 0.6126 seconds. 0.448578 is the ballistic projectile time. 1.062 is the time to travel the same distance at the speed of sound The MEASURED, absolute value, of the Ellapsed Time difference, per the audio amplitude graph... ...between the Last Bullet sound event and the Last Report sound event is 0.689655 Now, ask your donkey - what distance does that MEASURED absolute time difference correspond to on the chart?
No Absolute value is ever expressed as a negative number. Had your undisclosed formula for the last column of your spreadsheet included code to express an absolute value, your spreadsheet results would not appear as negative numbers. But your spreadsheet displays negative numbers and you did not even question it or fix your spreadsheet. The results should all be positive, like this: d = distance 400 yards, 1200 feet Column 1 = d/FPS = time in seconds Row 1 = directly inserted data. Data display is set to show 3 decimal places. Row 2 = spreadsheet formulas The formulas for Row 2 are dragged down to generate Rows 3-30.
>>No Absolute value is ever expressed as a negative number. =========== Since we KNOW from the observed audio Vb is supersonic, we can treat the difference between Tb and Ts as Absolute. Range corresponds to the ABSOLUTE value of the difference in time.
And BTW, You're not even reading from the relevant part of the paper - where the microphone adjacent to the victim scenario is discussed. http://ww w.btgresearch.org/AcousticReconstruction02042012.pdf That's the same formula I have in my illustration:
I know. They have a spreadsheet function for that. It has been around since Lotus 123 and Quatro. ABS(number).
Yes, but in this case the ABS is implied in knowledge of what the spreadsheet is actually calculating. If you applied ABS(Tb-Ts-) the chart would loose the information regarding whether the Vb was super-sonic or not, which the negative numbers conveniently tell us. The author's formula works just fine without your tweakage. http://ww w.btgresearch.org/AcousticReconstruction02042012.pdf And that IS the same formula I have in my illustration:
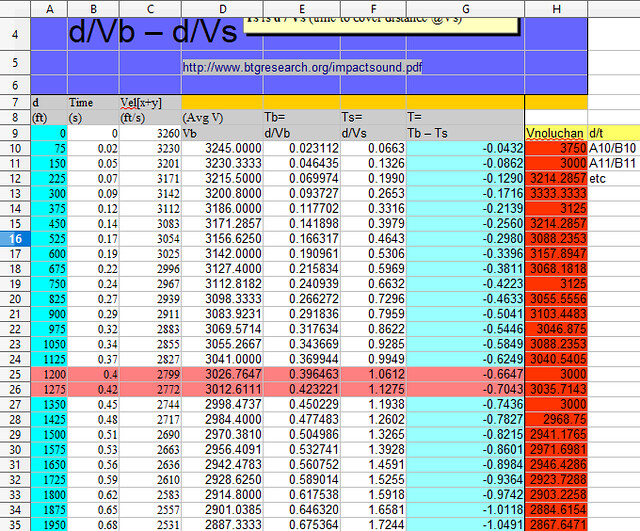
Why do you keep posting this chartoon when all your data is not only wrong, but farcical? The only things you proved is that you do not know how to calculate the average velocity of an imaginary bullet and you are hopeless at spreadsheets. Your entertainment value as a useful idiot is over for now, and you will never figure it out without more help. Help is on the way, grasshopper. Columns 1, 2, and 3 are direct entry of data generated by entering imaginary data into a generator at http://www.shooterscalculator.com/. I replicated the data taken from the calculator with “My BB's.” If I input initial velocity as 3240 fps, and other data, and call it “My BB's,” I can show a chart for magical bb’s. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 The Shooter’s Calculator only provides a result based on user input. It does not present a spreadsheet with the formulas to generate the data. The data from the Calculator can be cut and pasted into a spreadsheet, or entered by direct entry; this produces data in the cells, but no spreadsheet formulas in the cells. The chart states the speed of sound as 1130 feet per second (fps). The remaining 4 columns, (4, 5, 6, 7) were generated by VxH. Column 6 uses 1130.8 fps to calculate the time for sound to travel the distance stated in Column 1. Column 4 is labeled as (Avg V) Vb. This column purports to present the average velocity of the bullet to cover the distance for the row it is in. All of the data in this column is epically wrong as the methodology of calculation is absurdly wrong. To calculate the average velocity of the bullet, divide distance by time. Instead of this, a personal misbegotten formula was used. Probably a pocket calculator for each cell in Column 4 was used to perform the calculations, and the data was directly entered into the cells by hand. For the first two data rows, sum 3240 and 3163 and divide by 2. 6403/2 yields the 3201 in Column 4. For the first three data rows, sum 3240+3163+3088 for 9491. 9491 / 3 yields the 3163.6667 in Column 4. And so on, and so forth. All the calculated Column 4 data (average Vb), is garbage. The chosen methodology was to sum the velocity given for each distance, and divide by the number of elements summed. This produces nonsensical data. Example: You drive a car 100 miles at 80 mph. You drive another 100 miles at 20 mph. With this bogus methodology, 80 + 20 = 100, divide by 2, and your average velocity was 50 mph. Not. In the real world, you drove 100/80 or 1.25 hours at 80 mph. You drove 100/20 or 5 hours at 20 mph. And you drove 200 miles in 6.25 hours. Your average speed was 200/6.25, or 32 mph. Column 4, in addition to using an absurd methodology for its calculations, also incorporates two summing errors for the velocities taken from Column 3, at 900 feet and 1275 ft. In each case, the actual sum was 1 less than that calculated. Spreadsheet formulas are not prone to fat finger syndrome, and do not make such errors, but someone with a pocket calculator or pen and paper does. The data was typed in after external calculation. Where you calculate 2367.5926 average Vb at 1950 feet, 1950/1.211933 (the velocity of the bullet in Column 5), it yields 1608.9998 fps, remarkably close to the 1609 in Column 3. But then, the elapsed time in Column 2 is 0.86, not 1.21933. It is a conundrum how the bullet traveled for 1.21933 seconds in an elapsed time of 0.86 seconds. Of course, when you use Column 1 1950 ft and Column 3 1609 fps to derive the time of flight, the formula is d/Vb, and Vb is the Average Velocity. The bullet will travel 1905 feet distance (Col 1) in 0.86 sec time (Col 2) in 1905/0.86 or 2267.4418 average Vb. Stated in your headnote is Tb is d/Vb. It is noteworthy that you used Column 3 as the "average" velocity of the bullet in order to derive the other average velocity of the bullet in Column 4. Column 5 (Tb) incorporates the garbage data from Column 4 into its calculations, and all the resulting calculated data is wrong. GIGO. Column 7 (T = Tb – Ts) incorporates the garbage data from Column 5 and all the calculated data is wrong. GIGO. The chart is multicolor and pretty, but the data for the imaginary bullet is demonstrably wrong in every column you created, except for column 6 where you succeeded in dividing the distance by 1130.8.
LOL please tell the class why the bullet accelerates / decelerates / accelerates repeatedly when your "analysis" is applied? The time in the chart rendered by the ballistic calculator only has 2 decimals of precision. Calculating the average per the reported velocity is thus more accurate.
>> and the data was directly entered into the cells by hand. Bzzzt. Fail again.
Some dirty rotten no good chopped the formulas off your chart. d is the target distance.(range) The time in the chart rendered by the ballistic calculator only has 2 decimals of precision. Calculating the average per the reported velocity is thus more accurate. More accurate is to divide the distance by the velocity and get the time to more decimal places and eliminate the rounding error. Your bullshit methodology of summing velocities and dividing does not work. It is bullshit. Your chart in Column 2 from btgresearch indicates Tb for range 1950 is 0.86 seconds. Column 5 for 1950 range indicates Tb is 0.823621. You call that fixing a rounding error???? How did displaying only two decimal places to 0.86 convert to 0.823621. Of course, the time of 0.02 could represent a figure rounded to two decimal places for presentation, and actually represent anything from 0.0150 to 0.0249. 75 feet divided by Vel[x] 3239 75/3239 feet, taken to six decimal places gives 0.0231552 seconds bullet travel time. Hot damn, it's within the rounding error. At Vel[x+y] 3240 feet per second, and 75 feet distance, the time to six decimal places would be 0.0231481 seconds bullet travel time and hot damn, that's within the rounding error too. You have the distance and velocity as a given from btgresearch. Divide the distance by the velocity d/V, and you can calculate the time to however many decimal places you desire. The stupid... it hurts! The chart results are based on the data you entered. As I demonstratred, the same data entered for My BB's produces a chart with the same data for BB's. If the chart correctly calculated the ballistic data for the parameters you entered, http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 Tell everybody how you derived average velocity. Come on. Question my analysis of how you made a botch of the Average Bullet Velocity. Give us your methodology and formula. Why were all your calculations wrong except for distance divided by time? The data which you input did not come from any real life ammunition, you just entered stuff, as I did for My BB's. I just entered the same stuff you did, proving my bb's have an initial Vel[x+y] of 3240 fps. My BB's perform precisely as do your imaginary cartridge. Are you saying the ballistics chart you used produced invalid results? If the chart results are valid, please tell the class why the chart indicates the bullet traveled 75 ft. in 0.02 seconds and that indicates average velocity d/time of 750/.02 = 3750 fps. It's your data. If the ballistics chart calculated correctly, you should understand the chart you presented, and be able to explain the results given. Do you think you are entitled to just use a nonsense formula which produces nosense results because you do not understand the chart data that you selected and presented? The note at the bottom of the chart indicates: Thank you, Lord.
Bzzzt. Fail again. Nope. You said you created spreadsheet and used their formulas. Had you used their formulas you would not have bullshit results, including arithmetic errors in the columns. Which formula of theirs did you use to manufacture the wrong bullet velocities? Cite any source that says to find average velocity with the method you used. When you introduced this bullshit on the other thread at your #19 to A K A Stone, you said: https://libertysflame.com/cgi-bin/readart.cgi?ArtNum=53046&Disp=19#C19 Only you did not use their formulas or you would not have gotten all the data you derived bass ackwards wrong, and you did not create formulas and drag them down through the rows, or you would not have the calculation errors the are apparent. I created a spreadsheet using the same data and created formulas and dragged them down through the rows. They work. That is how I can pinpoint where you made calculating errors in your data entry. All you did was cut and paste the chart data into a spreadsheet workbook. Columns 1 thru 3 were cut and paste. For Column 4, there is no chance that you created a formula and dragged it down through the rows. You go off at range 900 where you summed to 36497 instead of 36496. This error of 1 continues through to range 1275, where you summed to 47,572 instead of 45,570. This put the summing error at 2, which continued through range 1950 where you ended. This is not a spreadsheet error. I used two different formulas to sum the velocities, with results identical to each other. You used no formula. You sat there with your pocket calculator and added the first two and typed in the result. Then you added the third velocity and typed in the result. And you did this for each data entry in that column. If you have any spreadsheet formula that can replicate your results, produce it. As Column 4 calculates the sum of the velocities divided by the number of velocities, and the sum of the velocities was not created by a formula on a spreadsheet column, the column was manual data entry. In Column 5, d/Vb, the distance is correctly divided by the bogus average velocity, yielding a bogus result. When it is as simple as programming one column divided by another, good job. When it is summing a changing number of rows, fuhgetaboutit. That was direct data entry with arithmetic errors. In Column 6, I stated you were able to divide distance by 1130.8. When it is summing a changing number of rows, fuhgetaboutit. That was direct data entry with arithmetic errors. In Column 7, you managed to correctly subtract the bogus data in Column 5 from the bogus data in Column 6, yielding all bogus results. When it is as simple as programming one column subtracted from another, good job. It should have included an ABS function to avoid getting negative time results.When it is summing a changing number of rows, fuhgetaboutit. That was direct data entry with arithmetic errors. As Columns 5 and 7 incorporate the brain dead data in Column 4, with a double whammy of a bogus formula and calculation errors, all data in Columns 5 and 7 is bogus. Your chart in Column 2 from btgresearch indicates Tb for range 1950 is 0.86 seconds. Column 5 for 1950 range indicates Tb is 0.823621. You call that fixing a rounding error???? How did displaying only two decimal places to 0.86 convert to 0.823621????
As Column 4 calculates the sum of the velocities divided by the number of velocities, and the sum of the velocities was not created by a formula on a spreadsheet column, the column was manual data entry. Bzzzt. Another Nolu-FAIL. =SUM(C9:C10)/L9 Now please tell us how Nolu-Time works and then explain why the values of Column J are closer to Time (Column B) than Nolu-Time(Column I)? "more accurate is to divide the distance by the velocity and get the time to more decimal places nolu chan posted on 2017-10-28 18:47:52 ET https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53025&Disp=153#C153
Chan is kicking your ass and you are looking foolish with all your errors.
How do you determine your opinion?
I correctly illustrate the flaw inherent in taking a momentary point velocity of a continuously decelerating proctile and ASSuming it to be an average. There's a question regarding whether the value of Vel[x+y] for a given 75ft vector segment is the average Velocity OR whether it's just the momentry V at point d. Here is the spreadsheet updated with Tcalc where Tcalc is an attempt to reconstruct the elapsed Time for a given Vector: We're moving in the right direction - but the calculation for Tcalc could be even more accurate by deriving it from the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment, rather than taking momentary V at point d and ASSuming it's a constant velocity over the entire 75ft segment... like you are.
Says the genius who posts videos with scribbling on a whiteboard presented as "PROOF". Can you solve for T given a 75 foot vector having Vmin and Vmax? Let's see if Noluchan's donkey can!
Post some more goofy Klingon pics It enhances your credibility.
My Klingon pics succinctly illustrate the gullible nature of individuals who post videos with scribbling on a white board as "proof". How's that workin' for ya? Meanwhile: Q: Can you solve for T given a 75 foot vector having Vmin and Vmax?
You have repeatedly changed and modified your numbers. Could you provide me a list of all of your errors that you posted so I can remove them from the site so people don't look at bullshit?
Here is an analogy of your "proof" Blue 42 Blue 42 hut hut hike. Ok I proved you are wrong.
My mind it is a beautiful thing.
I see your problem, now; it is called, profane vanity.
So you are with the V guy. That''s ok You agree with his analysis 100 percent correct. Or is your mind superior like mine and know that his analysis is bullshit. To many errors. To many things not factored in. I'm not saying that there were multiple shooters. I'm not saying Pollock or Paddock or whatever his name was didn't act alone. I'm just saying what V dude offers as 100 percent conclusive proof is not conclusive or proof.
Says the genius who made up an image with lots of wrong and made up numbers. I know the truth know. Spock is controlling your mind.
Truth is great and will prevail unless deprived of her natural weapons, free argument and debate. Does that work in AKA Stoned Land? There's nothing wrong with refining an analysis in the context of an honest desire to seek the truth. Time is still not being calculated with 100% accuracy. Why is that?
Does that work in AKA Stoned Land? That is fine. Truth also works if false things are no longer out there. If you care about truth why don't you find a list of all the posts yoy made with errors so we can correct them with the latest and the greatest.
In this case, the truth is still a work in process. For the next step in the process - Maybe "yoy" and Noluchan's donkey can tell us why applying a linear calculation (d/v) to a non-linear velocity produces values for Time which are farther away from the Ballistic chart's value for T than rounding can explain?
ROTFL
So, Illustration A: Vb calculated from d/Tcalc, where Tcalc= (d=75ft)/Vel A: Please explain how, in the context of the highlighted range of interest on the concert field, Noluchan's idea to reconstruct Time by taking (d=75ft)/Vel[x+y] Feel free to consult Noluchan's Donkey, since it probably has better temperament and reading comprehension skills than either of you two have demonstrated.
There's a question regarding whether the value of Vel[x+y] for a given 75ft vector segment is the average Velocity OR whether it's just the momentry V at point d. The problem is that you are clueless and do not know what your are doing and do not know what a vector is. Here is a correct spreadsheet: As a vector is described by a line and not a point, the Column D velocity at 75 feet describes the average bullet velocity for the segment from 0 to 75 feet, and the velocity at 150 feet describes the average bullet velocity from 0 to 150 feet, and so on. The time for 75 feet indicates the elapsed time for 0 to 75 feet. The time for 150 feet indicates the elapsed time for 0 to 150 feet. Column C, the time, is derived by dividing Column B (distance) by Column D. In your chart it is was rounded off to two decimal places. I took it to four decimal places. Your added Rube Goldberg nonsense was not only wrong but unecessary. Average velocity at the stated distances was staring you in the face. In Columns H thru L, I have provided the data for each 75-foot segment. At 1575 feet, the bullet opens its largest gap on sound at 0.05502 seconds. From 1575 to 1650 feet, the bullet travels at an average velocity of 1127.9144 fps, dipping below the speed of sound. After that, sound is traveling faster than the bullet and the gap diminishes.
>>Here is a correct spreadsheet Too bad it's not one you created with ballistic data as per the methodology: http://www.btgr esearch.org/AcousticReconstruction02042012.pdf Meanwhile, Please explain how, in the context of the highlighted range of interest on the concert field, Your idea to reconstruct Time by taking (d=75ft)/Vel[x+y] does not seem to produce results that magically render the values produced by summing and averaging Vel[x+y] into " bullshit" Illustration A: Vb calculated from d/Tcalc, where Tcalc= (d=75ft)/Vel A: Please explain how, in the context of the highlighted range of interest on the concert field, Noluchan's idea to reconstruct Time by taking (d=75ft)/Vel[x+y]
It surprises me a little that we have seen no attempts at forensic reconstruction of the shooting by recognized shooting experts and/or audio experts. Other than that sad-sack attempt by the NYSlimes, I haven't seen anything along these lines. There are experts out there. So why aren't we hearing from them? Is it because they find the audio data to be ambiguous? Who knows.
I asked the authors of the study http://www.btgresearch.org/AcousticReconstruction02042012.pdf They replied: "our standard operating procedure is to avoid public comments on shooting events. This better protects our neutrality and value of our analysis in the event that we are retained by an agency or party to subsequent legal proceedings. We also like to restrict our analysis to materials that come into our possession following a proper and documented chain of custody regarding handling of evidence. When it comes time for depositions or courtroom testimony, most experts who have made prior public comments on a matter find that opposing legal counsel, opposing experts, and the blogosphere find ways to make them regret earlier public comments." =============== In light of what can be observed here - that makes sense.
Well, it is an explanation. They're hoping to be hired guns as expert witnesses in the upcoming civil litigation.
Yeah. In the meantime, I've found this exercise to be a worthwhile learning experience.
At 1950 ft your "spreadsheet" has an elapsed time of 1.2119 with a corresponding Vel[x+y] of 1609. Meanwhile observe the corresponding elapsed time and Vel[x+y] generated by: OOPS! How'd ya manage to do that, Professor DonkyChan?
I'm not telling you to stop or that you're wasting your time. You might stumble over something unnoticed by everyone. Recall how Dan Rather was brought down by a persistent guy that noticed the fonts in the fake documents about Dumbya's military service.
If your Column c, Vel[x+y] (ft/s) represents an instantaneous velocity, it cannot be used in this manner. Make up your mind, does Column C represent instantaneous velocities, valid only at a single point, and not over any range?
Says the Donkey who managed to transform 0.86 seconds into 1.2119 seconds. Meanwhile... http://www.answers.com/Q /What_is_instantaneous_slope As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment.
http://www.answers.com/Q /What_is_instantaneous_slope As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment. To find what is at your source, we go to the link, which, like the link to the Khan Academy, only shows that you are bullshitting. You seem to have a special affinity in providing cut and paste bullshit as as some sort of profound knowledge. http://www.answers.com/Q/What_is_instantaneous_slope The instantaneous slope of a curve is the slope of that curve at a single point. In calculus, this is called the derivative. It also might be called the line tangent to the curve at a point. If you imagine an arbitrary curve (just any curve) with two points on it (point P and point Q), the slope between P and Q is the slope of the line connecting those two points. This is called a secant line. If you keep P where it is and slide Q closer and closer to P along the curve, the secant line will change slope as it gets smaller and smaller. When Q gets extremely close to P (so that there is an infinitesimal space between P and Q), then the slope of the secant line approximates the slope at P. When we take the limit of that tiny distance as it approaches zero (meaning we make the space disappear) we get the slope of the curve at P. This is the instantaneous slope or the derivative of the curve at P. Mathematically, we say that the slope at P = limh—>0 [f(x+h) - f(x)]÷h = df/dx, where h is the distance between P and Q, f(x) is the position of P, f(x+h) is the position of Q, and df/dx is the derivative of the curve with respect to x. The formula above is a specific case where the derivative is in terms of x and we're dealing with two dimensions. In physics, the instantaneous slope (derivative) of a position function is velocity, the derivative of velocity is acceleration, and the derivative of acceleration is jerk. Of course, the calculus formula P = limh—>0 [f(x+h) - f(x)]÷h = df/dx, where h is the distance between P and Q, f(x) is the position of P, f(x+h) is the position of Q, and df/dx is the derivative of the curve with respect to x was not used anywhere in your spreadsheet, so you are just bullshitting. Also, However, the slope of a bullet in flight is constantly changing, the deceleration is not constant, and the slope contains an infinite number of points. Moreover, you have merely bullshitted and have not described any formula to obtain the average velocity of the bullet over a given range, using instantaneous velocities. While you claim calculus formulas in your spreadsheet, you have yet to show a formula to sum changing parts of a spreadsheet column, i.e., sum row 1 and 2, sum row 1 thru 3, then row 1 thru 4, and so forth. I used such a formula and it showed that your column contained arithmetical errors not created by a spreadsheet formula. When you can program adding sums, I'll consider you doing calculus. As it is, you have not demostrated the ability to consistently add two numbers together, which is what you did to to sum that column. You added rows 1 and 2 to get the row 2 total; then you added row 3 to get the row 3 total, and so on, making two errors in 26 rows. You are fortunate it was now a thousand rows on a spreadsheet in a finance office. The formula for calculating average velocity (d/t) is given by the Khan Academy in the video you referenced. In their example, they divide a distance fo 1000m by 200s and get an average velocity of 5 m/s, and then they explicitly state, that siad result "doesn't necessarily equal the instantaneous velocities at particular points." The Khan Academy does not say that you can sum two instantaneous velocities and divide by two, and get an average velocity between the two points. See what you referenced. The first sentence is important — pretend you are a physics student. - [Instructor] Pretend you are a physics student. You are just getting out of class. You were walking home when you remembered that there was a Galaxy Wars marathon on tonight, so you'd do what every physics student would do: run. You're pretty motivated to get home, so say you start running at six meters per second. Maybe it's been a while since the last time you ran, so you have to slow down a little bit to two meters per second. When you get a little closer to home, you say: "No, Captain Antares wouldn't give up "and I'm not giving up either", and you start running at eight meters per second and you make it home just in time for the opening music. These numbers are values of the instantaneous speed. The instantaneous speed is the speed of an object at a particular moment in time. And if you include the direction with that speed, you get the instantaneous velocity. In other words, eight meters per second to the right was the instantaneously velocity of this person at that particular moment in time. Note that this is different from the average velocity. If your home was 1,000 meters away from school and it took you a total of 200 seconds to get there, your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip. In other words, let's say you jogged 60 meters in a time of 15 seconds. During this time you were speeding up and slowing down and changing your speed at every moment. Regardless of the speeding up or slowing down that took place during this path, your average velocity's still just gonna be four meters per second to the right; or, if you like, positive four meters per second. Just as your instantaneous velocity at two discrete and infinitesimal points can not be summed and divided by two to obtain average velocity, the instantaneous slope at two discrete and infinitesimal points will be different and cannot be used to calculate the slope of a traveling bullet whose velocity is contantly changing. While this bullshit about instantaneous slopes has diverted from your other bullshit about instantaneous velocities, you are still left searching to explain (1) your calculation used to derive average velocity over the specified distances, (2) your calculation used to change the formula for calculating average velocity over distance. Your chart stipulated distance and time. For 75 feet, you stipulated 0.02 seconds. This is your data, not mine. Using the formula, d/t=V(avg), that is 3,750 feet per second average velocity. If we assume that you meant the time to be anything between 0.015 and 0.025 seconds, that is 3000 - 5000 feet per second average velocity. For 1950 feet, you stipulated 0.86 seconds, and an average velocity of 2367.5926 feet per second, obtained by a formula you can neither present nor explain, nor can you provide any citation to any authority for your bullshit calculation. V(avg) = d/t = 1950/0.86 = 2267.4418 feet per second average velocity. If we assume that you meant the time to be anything between 0.855 and 0.865, then, V(avg) may equal 1950/0.0855 = 2280.7017 V(avg) may equal 1950/0.0865 = 2254.3353 Meanwhile, your bullshit 2367.5926 average velocity allows one to derive the time required to travel 1950 feet. 1950/2367.5926 = 0.823621429 seconds. Indeed, your second time for Tb, the time of the bullet, in your column E, reflects a bullet flight time of 0.823621 seconds, giving three less decimal points than I did, but rounding the the same precise thing at your chosen four decimal places, indicating how you derived that bullshit Tb from the bullshit average velocity. To check whether this bullshit time is not impossible with the stipulated data, one need only check if it is within the rounding possibilities of the stipulated data, i.e., from 0.855 to 0.865 seconds. Oh noes, your bullshit average velocity (0.823621) is not possible to reconcile with the stiplulated time, even allowing for the maximum rounding error. Your misbegotten time would round to 0.82 instead of 0.86. You have yet to explain how you can stipulate a bullet time of 0.86 seconds, and through the magic of VxH formulas, transform that time into 0.823621 seconds, and then use that visibly bullshit time to perform further bullshit calculations. If the bullet flew 1950 feet in 0.823621, why sure enough it went at an average velocity of 2367.5938 and covered 1950 feet. However, at the stipulated time of 0.86 seconds, at the bullshit average velocity of 2367.5938 feet per second, the bullet would have flown 2036.1307 feet. The stipulated distance is 1950 feet. At the maximum rounding down error to 0.855 seconds, at your bullshit average velocity of 2367.5926, the bullet would have flown 2024.292699 feet (0.855 x 2367.5926). The stipulated distance is 1950 feet. With your stipulated data, you may not have more or less than 1950 feet. You may not have less than 0.855 seconds flight time, nor more than 0.865 seconds flight time. You cannot change the distance the bullet flew, nor do more than consider a rounding error on the time. Your calculated numbers fail miserably. Your bullshit calculated numbers fall outside the maximum possible error attributable to a rounding error. Your bullshit calculations result in a new time, not within any rounding error, replacing 0.86 with 0.823621. Your bullshit average velocity over 1950 feet (2367.5926), at the maximum rounding error for stipulated time (0.86 rounded down to 0.855), requires the bullet to fly a minimum of 2024.292699 feet.
Comments (131 - 148) not displayed.
Top • Page Up • Full Thread • Page Down • Bottom/Latest Maybe you just don't have what it takes.
#91. To: nolu chan (#90)
(Edited)
#92. To: VxH (#91)
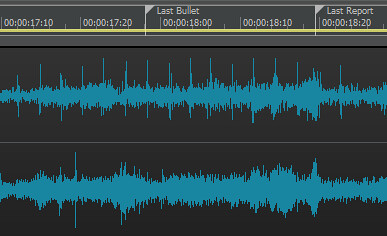
Now, ask your donkey - what distance does that MEASURED absolute time difference correspond to on the chart?
Bullet Time, Velocity FPS, Tb–Ts
Tb = Time of bullet
Ts = Time of sound, 1.062 seconds @ 1,130 feet per second (FPS) (72ºF, 20% Humidity)
Ts – Tb = Time difference between Tb and Ts
Column 2 = Tb stepped in 100 FPS increments, beginning with Ts
Column 3 = Ts – Tb (time in seconds supersonic bullet arrives ahead of sound) Bullet time (s), Bullet average velocity (FPS), time difference to sound at 1,200 feet (s)
Bullet time (s) Bullet average vel FPS Time diff Ts-Tb 1.062 1130 0.000 0.976 1230 0.086 0.902 1330 0.160 0.839 1430 0.223 0.784 1530 0.278 0.736 1630 0.326 0.694 1730 0.368 0.656 1830 0.406 0.622 1930 0.440 0.591 2030 0.471 0.563 2130 0.499 0.538 2230 0.524 0.515 2330 0.547 0.494 2430 0.568 0.474 2530 0.588 0.456 2630 0.606 0.440 2730 0.622 0.424 2830 0.638 0.410 2930 0.652 0.396 3030 0.666 0.383 3130 0.679 0.372 3230 0.690 0.360 3330 0.702 0.350 3430 0.712 0.340 3530 0.722 0.331 3630 0.731 0.322 3730 0.740 0.313 3830 0.749 0.305 3930 0.757 0.298 4030 0.764
#93. To: nolu chan (#92)
(Edited)

#94. To: nolu chan (#92)
(Edited)


#95. To: VxH (#93)
Since we KNOW from the observed audio Vb is supersonic, we can treat the difference between Tb and Ts as Absolute.
#96. To: nolu chan (#95)
(Edited)
They have a spreadsheet function for that.


#97. To: VxH (#96)

#98. To: nolu chan (#97)
(Edited)
#99. To: nolu chan (#97)
(Edited)
Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fpsRange Time Vel[x+y] (ft) (s) (ft/s) 0 0.00 3240 75 0.02 3163 150 0.05 3088 225 0.07 3014 300 0.10 2941 375 0.12 2870 450 0.15 2799 525 0.18 2730 600 0.20 2662 675 0.23 2595 750 0.26 2529 825 0.29 2465 900 0.32 2401 975 0.36 2337 1050 0.39 2275 1125 0.42 2214 1200 0.46 2154 1275 0.49 2095 1350 0.53 2036 1425 0.56 1979 1500 0.60 1923 1575 0.64 1867 1650 0.68 1813 1725 0.73 1760 1800 0.77 1708 1875 0.81 1658 1950 0.86 1609 2025 0.91 1561 2100 0.96 1515 2175 1.01 1470 2250 1.06 1426 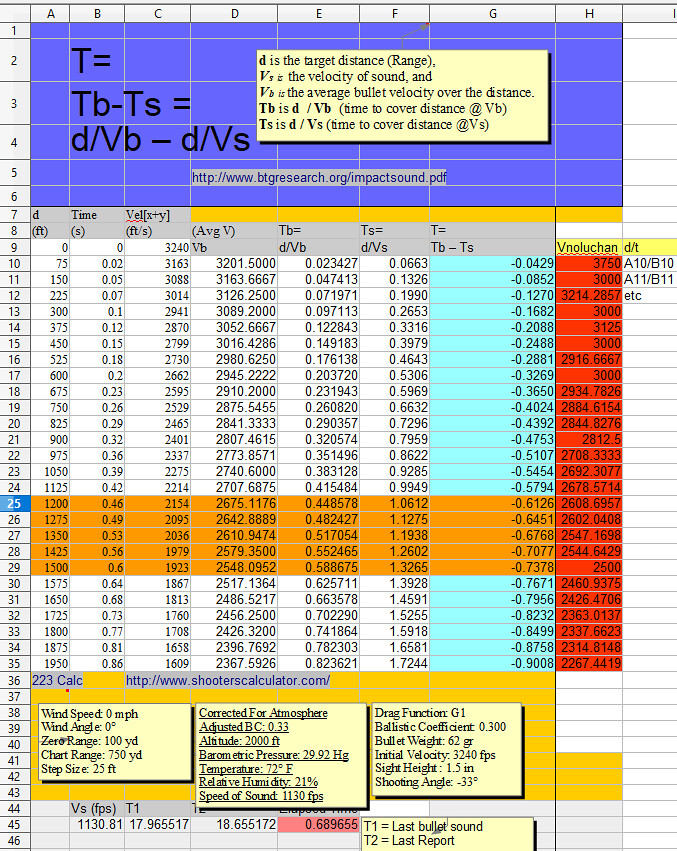

#100. To: VxH (#98)
Vs is the velocity of sound, and
Vb is the average bullet velocity over the distance
Tb is d / Vb (time to cover distance @ Vb)
Ts is d/Vs (time to cover distance @Vs) LOL please tell the class why the bullet accelerates / decelerates / accelerates repeatedly when your "analysis" is applied?
Keep in mind this is an approximation....
#101. To: VxH, A K A Stone (#99)
and the data was directly entered into the cells by hand.
I found/took their formula, built a spreadsheet, and plugged in 223 balistic data generated via shooterscalculator.com:
#102. To: nolu chan (#101)
(Edited)
=SUM(C$9:C11)/L10
=SUM(C$9:C12)/L11
etc.
Where column L contains 1 @ row 8 and =+L8+1, =+L9+1 etc for rows 9..34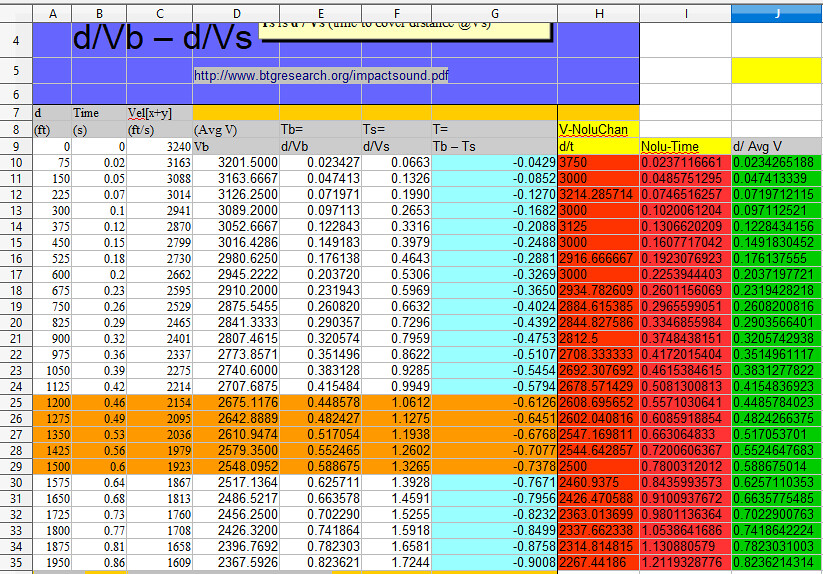
#103. To: VxH (#102)
#104. To: A K A Stone (#103)
#105. To: nolu chan (#101)
(Edited)
You stipulate a DISTANCE ratio of 99:1. Nice try.

#106. To: A K A Stone (#103)
Chan is kicking your ass and you are looking foolish with all your errors.
#107. To: VxH (#106)
#108. To: A K A Stone (#107)
(Edited)
A: { crickets crickets crickets }
#109. To: VxH (#108)
#110. To: VxH (#108)
#111. To: buckeroo (#104)
How do you determine your opinion?
#112. To: A K A Stone (#111)
#113. To: buckeroo (#112)
#114. To: VxH (#106)
(Edited)
Says the genius who posts videos with scribbling on a whiteboard presented as "PROOF".

#115. To: A K A Stone (#109)
#116. To: VxH (#115)
(Edited)
Truth is great and will prevail unless deprived of her natural weapons, free argument and debate.
#117. To: A K A Stone (#116)
(Edited)
If you care about truth why don't you find a list of all the posts yoy made with errors
#118. To: VxH, A K A Stone, noluchan (#117)
Maybe you and Noluchan's donkey can tell us why applying a linear calculation (d/v) to a non-linear velocity produces values for Time which are farther away from the Ballistic chart's value for T than rounding can explain?
#119. To: A K A Stone, noluchan, buckeroo (#117)
(Edited)
{ crickets crickets crickets }
Illustration B: Vb using my original Average of summed Velocity values. B:
B: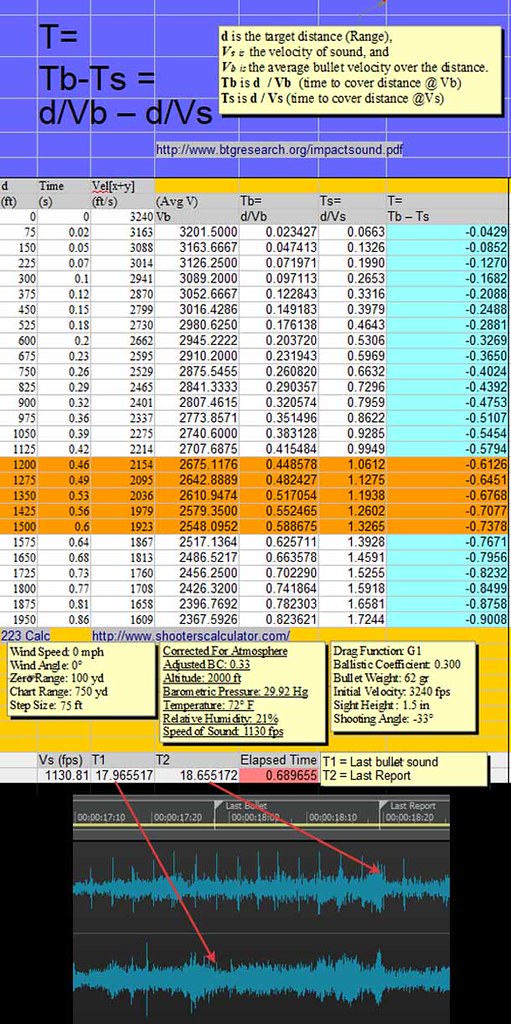
does not seem to produce results that magically render the values produced by summing and averaging Vel[x+y] into "bullshit"?
#120. To: VxH, A K A Stone (#105)
I correctly illustrate the flaw inherent in taking a momentary point velocity of a continuously decelerating proctile and ASSuming it to be an average.
BALLISTICS DATA SPREADSHEET
A1 AVERAGE VELOCITY AND TIME DIFF OVER TOTAL DISTANCE AVERAGE VELOCITY FOR EACH 75 FEET SEGMENT 2 3 B C D E F G H I J K L 4 d Time (avg) Vel[x+y] Ts=d/Vs T=Tb - Ts Tb 75 ft Avg Velocity for Segment Segment Segment 5 (ft) d/Vel[x+y] (ft/s) d/Vs ABS(Tb-Ts) +C7-C6 75 foot segment distance begin end 6 0 0.0000 3240 +75/H4 +B7-B6 +K7+75 A7 7 75 0.0237 3163 0.0664 0.0427 0.0237 3163.0000 75 0 75 8 150 0.0486 3088 0.1327 0.0842 0.0249 3016.4744 75 75 150 9 225 0.0747 3014 0.1991 0.1245 0.0261 2876.1533 75 150 225 10 300 0.1020 2941 0.2655 0.1635 0.0274 2741.7798 75 225 300 11 375 0.1307 2870 0.3319 0.2012 0.0287 2617.2620 75 300 375 12 450 0.1608 2799 0.3982 0.2375 0.0301 2490.8930 75 375 450 13 525 0.1923 2730 0.4646 0.2723 0.0315 2378.2353 75 450 525 14 600 0.2254 2662 0.5310 0.3056 0.0331 2266.7686 75 525 600 15 675 0.2601 2595 0.5973 0.3372 0.0347 2160.0657 75 600 675 16 750 0.2966 2529 0.6637 0.3672 0.0364 2057.9351 75 675 750 17 825 0.3347 2465 0.7301 0.3954 0.0381 1967.1773 75 750 825 18 900 0.3750 2400 0.7965 0.4215 0.0403 1860.3774 75 825 900 19 975 0.4172 2337 0.8628 0.4456 0.0422 1777.1863 75 900 975 20 1050 0.4615 2275 0.9292 0.4677 0.0443 1691.5924 75 975 1050 21 1125 0.5081 2214 0.9956 0.4874 0.0466 1609.7315 75 1050 1125 22 1200 0.5571 2154 1.0619 0.5048 0.0490 1531.4566 75 1125 1200 23 1275 0.6089 2094 1.1283 0.5194 0.0518 1448.4509 75 1200 1275 24 1350 0.6631 2036 1.1947 0.5316 0.0542 1384.2156 75 1275 1350 25 1425 0.7201 1979 1.2611 0.5410 0.0570 1315.8863 75 1350 1425 26 1500 0.7800 1923 1.3274 0.5474 0.0600 1250.6135 75 1425 1500 27 1575 0.8436 1867 1.3938 0.5502 0.0636 1179.8360 75 1500 1575 28 1650 0.9101 1813 1.4602 0.5501 0.0665 1127.9144 75 1575 1650 29 1725 0.9801 1760 1.5265 0.5464 0.0700 1071.1245 75 1650 1725 30 1800 1.0539 1708 1.5929 0.5391 0.0738 1016.9418 75 1725 1800 31 1875 1.1309 1658 1.6593 0.5284 0.0770 973.8184 75 1800 1875 32 1950 1.2119 1609 1.7257 0.5137 0.0811 925.3285 75 1875 1950 33 2025 1.2972 1561 1.7920 0.4948 0.0853 879.1211 75 1950 2025 34 2100 1.3861 1515 1.8584 0.4723 0.0889 843.7085 75 2025 2100 35 2175 1.4796 1470 1.9248 0.4452 0.0935 802.5405 75 2100 2175 36 2250 1.5778 1426 1.9912 0.4133 0.0982 763.3722 75 2175 2250 37 38 Total 39 1.5780 40 SUM G7:G36
#121. To: nolu chan (#120)
(Edited)
?
Illustration B: Vb using my original Average of summed Velocity values. B:
B:
does not seem to produce results that magically render the values produced by summing and averaging Vel[x+y] into " bullshit"?
#122. To: VxH (#121)
(Edited)
#123. To: Tooconservative (#122)
There are experts out there. So why aren't we hearing from them?
#124. To: VxH (#123)
#125. To: Tooconservative (#124)
Well, it is an explanation.
#126. To: nolu chan (#120)
(Edited)
4 d Time (avg) Vel[x+y] 5 (ft) d/Vel[x+y] (ft/s) 32 1950 1.2119 1609 1950 0.86 1609 Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%Range Time Vel[x+y] (ft) (s) (ft/s) 0 0.00 3240 75 0.02 3163 150 0.05 3088 225 0.07 3014 300 0.10 2941 375 0.12 2870 450 0.15 2799 525 0.18 2730 600 0.20 2662 675 0.23 2595 750 0.26 2529 825 0.29 2465 900 0.32 2401 975 0.36 2337 1050 0.39 2275 1125 0.42 2214 1200 0.46 2154 1275 0.49 2095 1350 0.53 2036 1425 0.56 1979 1500 0.60 1923 1575 0.64 1867 1650 0.68 1813 1725 0.73 1760 1800 0.77 1708 1875 0.81 1658 1950 0.86 1609 2025 0.91 1561 2100 0.96 1515 2175 1.01 1470 2250 1.06 1426
#127. To: VxH (#125)
Yeah. In the meantime, I've found this exercise to be a worthwhile learning experience.
#128. To: VxH, A K A Stone (#119)
Illustration A: Vb calculated from d/Tcalc, where Tcalc= (d=75ft)/Vel
#129. To: nolu chan (#128)
(Edited)
it cannot be used in this manner.
#130. To: VxH, A K A Stone (#129)
Meanwhile...
Answer byBlue
Confidence votes 38.3K When Q gets extremely close to P (so that there is an infinitesimal space between P and Q), then the slope of the secant line approximates the slope at P. When we take the limit of that tiny distance as it approaches zero (meaning we make the space disappear) we get the slope of the curve at P. This is the instantaneous slope or the derivative of the curve at P.
Video transcript
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
.
.
.
[Home] [Headlines] [Latest Articles] [Latest Comments] [Post] [Mail] [Sign-in] [Setup] [Help] [Register]
