United States News
See other United States News Articles
Title: Video claims shooter dressed as police
Source:
[None]
URL Source: https://duckduckgo.com/?q=LAS+VEGAS ... a=videos&iax=1&iai=qMxn7hpXmk4
Published: Oct 8, 2017
Author: Planet X Investigations
Post Date: 2017-10-08 15:41:01 by A K A Stone
Keywords: None
Views: 74013
Comments: 186
Video claims shooter dressed as police Poster Comment: Video claims shooter dressed as police
Post Comment Private Reply Ignore Thread
Top • Page Up • Full Thread • Page Down • Bottom/Latest
Comments (1-146) not displayed.
.
.
.
#147. To: VxH (#146)
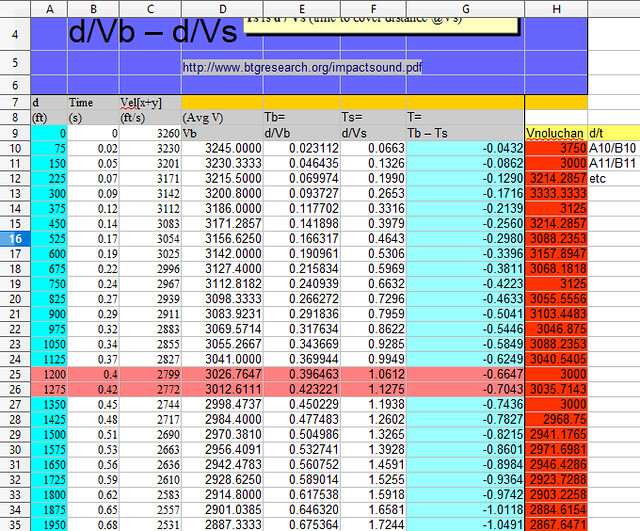
Why do you keep posting this chartoon when all your data is not only wrong, but farcical? The only things you proved is that you do not know how to calculate the average velocity of an imaginary bullet and you are hopeless at spreadsheets. Your entertainment value as a useful idiot is over for now, and you will never figure it out without more help. Help is on the way, grasshopper. Columns 1, 2, and 3 are direct entry of data generated by entering imaginary data into a generator at http://www.shooterscalculator.com/. I replicated the data taken from the calculator with “My BB's.” If I input initial velocity as 3240 fps, and other data, and call it “My BB's,” I can show a chart for magical bb’s. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 The Shooter’s Calculator only provides a result based on user input. It does not present a spreadsheet with the formulas to generate the data. The data from the Calculator can be cut and pasted into a spreadsheet, or entered by direct entry; this produces data in the cells, but no spreadsheet formulas in the cells. The chart states the speed of sound as 1130 feet per second (fps). The remaining 4 columns, (4, 5, 6, 7) were generated by VxH. Column 6 uses 1130.8 fps to calculate the time for sound to travel the distance stated in Column 1. Column 4 is labeled as (Avg V) Vb. This column purports to present the average velocity of the bullet to cover the distance for the row it is in. All of the data in this column is epically wrong as the methodology of calculation is absurdly wrong. To calculate the average velocity of the bullet, divide distance by time. Instead of this, a personal misbegotten formula was used. Probably a pocket calculator for each cell in Column 4 was used to perform the calculations, and the data was directly entered into the cells by hand. For the first two data rows, sum 3240 and 3163 and divide by 2. 6403/2 yields the 3201 in Column 4. For the first three data rows, sum 3240+3163+3088 for 9491. 9491 / 3 yields the 3163.6667 in Column 4. And so on, and so forth. All the calculated Column 4 data (average Vb), is garbage. The chosen methodology was to sum the velocity given for each distance, and divide by the number of elements summed. This produces nonsensical data. Example: You drive a car 100 miles at 80 mph. You drive another 100 miles at 20 mph. With this bogus methodology, 80 + 20 = 100, divide by 2, and your average velocity was 50 mph. Not. In the real world, you drove 100/80 or 1.25 hours at 80 mph. You drove 100/20 or 5 hours at 20 mph. And you drove 200 miles in 6.25 hours. Your average speed was 200/6.25, or 32 mph. Column 4, in addition to using an absurd methodology for its calculations, also incorporates two summing errors for the velocities taken from Column 3, at 900 feet and 1275 ft. In each case, the actual sum was 1 less than that calculated. Spreadsheet formulas are not prone to fat finger syndrome, and do not make such errors, but someone with a pocket calculator or pen and paper does. The data was typed in after external calculation. Where you calculate 2367.5926 average Vb at 1950 feet, 1950/1.211933 (the velocity of the bullet in Column 5), it yields 1608.9998 fps, remarkably close to the 1609 in Column 3. But then, the elapsed time in Column 2 is 0.86, not 1.21933. It is a conundrum how the bullet traveled for 1.21933 seconds in an elapsed time of 0.86 seconds. Of course, when you use Column 1 1950 ft and Column 3 1609 fps to derive the time of flight, the formula is d/Vb, and Vb is the Average Velocity. The bullet will travel 1905 feet distance (Col 1) in 0.86 sec time (Col 2) in 1905/0.86 or 2267.4418 average Vb. Stated in your headnote is Tb is d/Vb. It is noteworthy that you used Column 3 as the "average" velocity of the bullet in order to derive the other average velocity of the bullet in Column 4. Column 5 (Tb) incorporates the garbage data from Column 4 into its calculations, and all the resulting calculated data is wrong. GIGO. Column 7 (T = Tb – Ts) incorporates the garbage data from Column 5 and all the calculated data is wrong. GIGO. The chart is multicolor and pretty, but the data for the imaginary bullet is demonstrably wrong in every column you created, except for column 6 where you succeeded in dividing the distance by 1130.8.
BTW = The Elapsed time between T1 and T2 0.689655 is quite quite sufficient for debunking the title of the video "shooter dressed as police". Even without the ballistic data (which is calculated correctly for the parameters entered) - the difference between the bullet sound event and the report sound event puts the distance of the shooter at least 784 feet. Is the guy "dreesed as police" 784 feet away? NOPE. Video status = DEBUNKED.
Psst. Please tell the class why, using your calculation, at 75 ft, the bullet has ACCELERATED to 3750fps, decerates to 3000fps at 150 seconds... and then accelerates to 3214fps at 225 feet... etc accelerating and decelerating and accelerating. Is it a magic bullet? The time in the chart rendered by the ballistic calculator only has 2 decimals of precision. Calculating the average per the reported velocity is thus more accurate.
Which is only as valid as the improbable or impossible data you entered. As I demonstratred, the same data entered for My BB's produces a chart with the same data for BB's. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 Come on. Question my analysis of how you made a botch of the Average Bullet Velocity. Give us your methodology and formula. Why were all your calculations wrong except for distance divided by time?
>>Question my analysis of how you made a botch of the Average Bullet Velocity. LOL. OK - please tell the class why the bullet accelerates / decelerates / accelerates repeatedly when your "analysis" is applied? The time in the chart rendered by the ballistic calculator only has 2 decimals of precision. Calculating the average per the reported velocity is thus more accurate.
>> and the data was directly entered into the cells by hand. Bzzzt. Fail again. http://www.shooterscalculator.com/ballistic-trajectory-chart.php
- - - - - - - - - - [VxH #149] Please tell the class why, using your calculation, at 75 ft, the bullet has ACCELERATED to 3750fps, decerates to 3000fps at 150 seconds... and then accelerates to 3214fps at 225 feet... etc accelerating and decelerating and accelerating. Is it a magic bullet? [VxH #151] Calculating the average per the reported velocity is thus more accurate. More accurate is to divide the distance by the velocity and get the time to more decimal places and eliminate the rounding error. Your bullshit methodology of summing velocities and dividing does not work. It is bullshit. The stupid... it hurts! The chart results are based on the data you entered. As I demonstratred, the same data entered for My BB's produces a chart with the same data for BB's. If the chart correctly calculated the ballistic data for the parameters you entered, http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 Tell everybody how you derived average velocity. Come on. Question my analysis of how you made a botch of the Average Bullet Velocity. Give us your methodology and formula. Why were all your calculations wrong except for distance divided by time? The data which you input did not come from any real life ammunition, you just entered stuff, as I did for My BB's. I just entered the same stuff you did, proving my bb's have an initial Vel[x+y] of 3240 fps. My BB's perform precisely as do your imaginary cartridge. Are you saying the ballistics chart you used produced invalid results? If the chart results are valid, please tell the class why the chart indicates the bullet traveled 75 ft. in 0.02 seconds and that indicates average velocity d/time of 750/.02 = 3750 fps. It's your data. If the ballistics chart calculated correctly, you should understand the chart you presented, and be able to explain the results given. Do you think you are entitled to just use a nonsense formula which produces nosense results because you do not understand the chart data that you selected and presented? The note at the bottom of the chart indicates: Of course, the time of 0.02 could represent a figure rounded to two decimal places for presentation, and actually represent anything from 0.0150 to 0.0249. 75 feet divided by Vel[x] 3239 75/3239 feet, taken to six decimal places gives 0.0231552 seconds bullet travel time. Hot damn, it's within the rounding error. At Vel[x+y] 3240 feet per second, and 75 feet distance, the time to six decimal places would be 0.0231481 seconds bullet travel time and hot damn, that's within the rounding error too. Thank you, Lord. At my #108 I asked, That question met with resounding crickets. A mystery, wrapped in an enigma, hidden by a conundrum, is why, at 75 feet, the chart indicates Vel(x) = 3239, Vel (y) = 5.70, and Vel[x+y] = 3240. Whatever can that strange arithmetic be? You could have chosen to display Vel[x] or Vel[y], or Vel[x+y]. Why did you choose to display Vel[x+y] rather than say, Vel[x]? What is Vel[x], Vel[y], and Vel[x+y]?
LOL. So you're going to drive 99 miles at 2mph, then drive and 1 mile at 100mph. You're going to divide 100 miles by what 100mph? Here are the values of Nolu- Time calculated with your d/v brainstorm: Ooops! Congratulations! You "fixed" the rounding of 0.86 by transforming it into 1.2119328776 are you sure that works? LOL. I know what they mean on the Ballistic calculator. Don't you? Hint: They're Vectors. And speaking of Vectors: If we treated each 75 ft segment as a vector and then calculated time as a function of the relationship between 75ft and the difference between {Vn..Vn+1}... that might work a little better than your simple d/v idea.
You're going to divide 100 miles by what 100mph? No. You measuring bullets at 75 foot increments. It is the DISTANCE that in the segment and remains the same. That is why your bullshit does not work and your question is bullshit. You stipulate a DISTANCE ratio of 99:1. Nice try. It is not one distance and 99 times that distance. The distances on the chart are in precisely equal steps. By your misbegotten Rube Goldberg "formula," the bullet traveled The correct times, carried to seven decimal places, are, The bullets traveled the precise same distance in different times and velocities. The distance segments are precisely the same; the elapsed time and velocity changes. Over equal distances, your formula is still bullshit. If you drive 99 miles at 99 mph, and 99 miles at 1 mph, 99/99 = 1 hour and 99 miles at 1 mph. 99/1 = 99 hours Your average speed is not 100/2 50 mph. Your average speed is 198m/100h = 1.98 mph. Duhhhh. Hint: They're Vectors. I know. You just found out. You still did not explain why you used Vel[x+y] rather than Vel[x]. Simple d/v is not my idea. You stated the Column 5 formula as Tb = d/Vb. Your bullshit of summing the travel over one 75 foot segment with the travel time over the next 75 foot segment, and making believe that this is the formula to find the bullet average time of travel is still bullshit. You did a nice job of chopping the formulas off the graphic posted above. Chopping them off does not make them go away. They are stated as: d is the target distance.(range) Where is the bullshit formula that has you summing the elapsed times of segments and dividing by the number of segments to get the average velocity? You link to btgresearch and then put your own misbegotten formulas on the page, with your bullshit data, for an imaginary cartridge with imaginary properties tweaked to get the initial velocity you wanted at the time.
Anybody who actually understands the ballistic calculator doesn't need an explanation.
[duplicate]
>>Simple d/v is not my idea. Liar. "more accurate is to divide the distance by the velocity and get the time to more decimal places nolu chan posted on 2017-10-28 18:47:52 ET https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53025&Disp=153#C153 Nolu-Time as d/v = FAIL Which is column has values that closer to the values under Time? Column I: Nolu- Time Column J does.
>>speaking of Vectors...
The problem is that you are clueless and do not know what your are doing and do not know what a vector is. A vector is described by a line, not a point. Here is a correct spreadsheet: As a vector is described by a line and not a point, the Column D velocity at 75 feet describes the average bullet velocity for the segment from 0 to 75 feet, and the velocity at 150 feet describes the average bullet velocity from 0 to 150 feet, and so on. The time for 75 feet indicates the elapsed time for 0 to 75 feet. The time for 150 feet indicates the elapsed time for 0 to 150 feet. Column C, the time, is derived by dividing Column B (distance) by Column D. In your chart it is was rounded off to two decimal places. I took it to four decimal places. Your added Rube Goldberg nonsense was not only wrong but unecessary. Average velocity at the stated distances was staring you in the face. In Columns H thru L, I have provided the data for each 75-foot segment. At 1575 feet, the bullet opens its largest gap on sound at 0.05502 seconds. From 1575 to 1650 feet, the bullet travels at an average velocity of 1127.9144 fps, dipping below the speed of sound. After that, sound is traveling faster than the bullet and the gap diminishes.
At 1950 ft your "spreadsheet" has an elapsed time of 1.2119 with a corresponding Vel[x+y] of 1609. Meanwhile observe the corresponding elapsed time and Vel[x+y] generated by: OOPS! How'd ya manage to do that, Professor DonkyChan?
I have one question. You keep changing your numbers. But they still always fit with your pet theory. Why is that
Ballistic deceleration is a non-linear system. Calculations we're using to model the system are thus only approximations. Different functions and methods can be used to model the system with varying degrees of approximation. In this case, the data produced by ballistic chart generators like ShooterCalculator.com can be used as a reference for approximate comparison. For example - the modeled values for Time should approximately correspond to the chart's reference values for Time. Now ask Professor DonkeyChan why his calculation for time (1.2119 seconds at a distance of 1950ft and a Velocity of 1609fps) is so significantly different from the value for Time (0.86 seconds) in the ballistic chart at the same Distance (1950ft) and Velocity (1609fps)? 1609fps @ 1950ft would appear to be the INSTANTANIOUS velocity, BTW - not the average Velocity, as Professor DonkeyChan asserts.
I used the precise data you provided and applied the correct formula, d/t = average velocity. In the case that Column C contains instantaneous velocities, the data is unusable for calculation of average velocity, or to derive the time, to greater accuracy, or any result at all. If the data in Column C is instantaneous velocity, the only way to calculate the average velocity is d/t, and the result for 75 yards would be 3750. While your chart fails to indicate any rounding has been performed, it is apparent that .02s appears rounded to two digits. Allowing for the rounding error, the result could be anything from 3000 fps to 4999.99 fps. Note where the Khan Academy stated "your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip." Why are you using instantaneous velocities at particular points to misstate average velocity?
What pet theory? In all of his word salad, did he tell you his methodology to calculate the results for Average Velocity appearing in his Column D, or anyone else's methodology to calculate the Average Velocity appearing in his Column D? There is nothing quite like an approximation taken to four decimal places. There is reference to a model system. Have you seen a model system to calculate the results for the Average Velocity in Column D? Where did this model system come from, and what does this model system say? Is there a link to a model system to calculate the Average Velocity as performed in Column D? Is there a link to any such system, model, or function? While "different functions and methods can be used to model the system," have you seen any functions and methods that have been presented? What you see is VxH or yukon's implementation of his model system to babble and obfuscate. Assume the Velocities in Column C represent only the bullet velocity at the discrete time the bullet arrives at the Column A distance. His spreadsheet calculation results indicate that he made up his own formula, which is sum the velocity at 0 feet and the velocity at 75 feet and divide by 2. Sum the velocity given for one point, and that for another point, and divide by two to get the average velocity between the two. If that works for 0 and 75 feet, it should work even better for 0 and 1950 feet. Take velocity at 0 feet (3240 fps) and the velocity at 1950 feet (1609 fps), sum them (4849), divide by 2, and the result is 2424.5 fps average velocity for the range 0 to 1950 feet. Why is his Column D average velocity (2367.5926) result for 1950 feet 56 fps different? While "different functions and methods can be used to model the system with varying degrees of approximation," the link goes to a youtube video at the Khan Academy about instantaneous velocities — velocities at a single specific point. The video does not answer the question of how to calculate average velocity. It does sort of tell one how not to calculate average velocity. You do not have to watch it, there is a transcript. Note where it says, "your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip." If you want instantaneous velocities, and that is what is in Column C, we are not looking for a formula to calculate them. But we cannot use instantaneous velocities to derive average velocity. The Khan Academy does not say that you can sum two instantaneous velocities and divide by two, and get an average velocity between the two points. - [Instructor] Pretend you are a physics student. You are just getting out of class. You were walking home when you remembered that there was a Galaxy Wars marathon on tonight, so you'd do what every physics student would do: run. You're pretty motivated to get home, so say you start running at six meters per second. Maybe it's been a while since the last time you ran, so you have to slow down a little bit to two meters per second. When you get a little closer to home, you say: "No, Captain Antares wouldn't give up "and I'm not giving up either", and you start running at eight meters per second and you make it home just in time for the opening music. These numbers are values of the instantaneous speed. The instantaneous speed is the speed of an object at a particular moment in time. And if you include the direction with that speed, you get the instantaneous velocity. In other words, eight meters per second to the right was the instantaneously velocity of this person at that particular moment in time. Note that this is different from the average velocity. If your home was 1,000 meters away from school and it took you a total of 200 seconds to get there, your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip. In other words, let's say you jogged 60 meters in a time of 15 seconds. During this time you were speeding up and slowing down and changing your speed at every moment. Regardless of the speeding up or slowing down that took place during this path, your average velocity's still just gonna be four meters per second to the right; or, if you like, positive four meters per second. Say you wanted to know the instantaneous velocity at a particular point in time during this trip. In that case, you'd wanna find a smaller displacement over a shorter time interval that's centered at that point where you're trying to find the instantaneous velocity. This would give you a better value for the instantaneous velocity but it still wouldn't be perfect. In order to better zero-in on the instantaneous velocity, we could choose an even smaller displacement over that even shorter time interval. But we're gonna run into a problem here because if you wanna find a perfect value for the instantaneous velocity, you'd have to take an infinitesimally-small displacement divided by an infinitesimally-small time interval. But that's basically zero divided by zero, and for a long time no one could make any sense of this. In fact, since defining motion at a particular point in time seemed impossible, it made some ancient Greeks question whether motion had any meaning at all. They wondered weather motion was just an illusion. Eventually, Sir Isaac Newton developed a whole new way to do math that lets you figure out answers to these types of questions. Today we call the math that Newton invented calculus. So if you were to ask a physicist: "What's the formula for the instantaneous velocity?", he or she would probably give you a formula that involves calculus. But, in case some of you haven't taken calculus yet, I'm gonna show you a few ways to find the instantaneous velocity that don't require the use of calculus. The first way is so simple that it's kind of obvious. If you're lucky enough to have a case where the velocity of an object doesn't change, then the formula for average velocity is just gonna give you the same number as the instantaneous velocity at any point in time. If your velocity is changing, one way you can find the instantaneous velocity is by looking at the motion on an x-versus-t graph. The slope at any particular point on this position-versus-time graph is gonna equal the instantaneous velocity at that point in time because the slope is gonna give the instantaneous rate at which x is changing with respect to time. A third way to find the instantaneous velocity is for another special case where the acceleration is constant. If the acceleration is constant, you can use the Kinematic Formulas to find the instantaneous velocity, v, at any time, t. (electronic music) Video on YouTube Creative Commons Attribution/Non-Commercial/Share-Alike They talk about how to find instantaneous velocity. The first example does not apply because velocities are changing. The third example does not apply because the acceleration (or deceleration) is not constant, and the cited Kinematic formulas are used to find instantaneous velocity. For the third example, you need an x-versus-t graph. Seen one lately?
>>I used the precise data you provided and applied the correct formula, d/t = average velocity. That'd be the CORRECT, non-linear, data produced by the Ballistic calculator - which you obviously applied the WRONG, linear, formula to "calculate" time (1.2119 seconds at a distance of 1950ft and a Velocity of 1609fps) which is significantly different from the value for Time (0.86 seconds) in the ballistic chart at the same Distance (1950ft) and Velocity (1609fps). ShooterCalculator.com Says: ======================== Professor DonkeyChan says: 1.2119 seconds nolu chan posted on 2017-10-30 19:58:41 ET https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53025&Disp=160#C160 ======================== Meanwhile... http://www.answers.com/Q /What_is_instantaneous_slope As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment.
http://www.answers.com/Q /What_is_instantaneous_slope As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment. To find what is at your source, we go to the link, which, like the link to the Khan Academy, only shows that you are bullshitting. You seem to have a special affinity in providing cut and paste bullshit as as some sort of profound knowledge. http://www.answers.com/Q/What_is_instantaneous_slope The instantaneous slope of a curve is the slope of that curve at a single point. In calculus, this is called the derivative. It also might be called the line tangent to the curve at a point. If you imagine an arbitrary curve (just any curve) with two points on it (point P and point Q), the slope between P and Q is the slope of the line connecting those two points. This is called a secant line. If you keep P where it is and slide Q closer and closer to P along the curve, the secant line will change slope as it gets smaller and smaller. When Q gets extremely close to P (so that there is an infinitesimal space between P and Q), then the slope of the secant line approximates the slope at P. When we take the limit of that tiny distance as it approaches zero (meaning we make the space disappear) we get the slope of the curve at P. This is the instantaneous slope or the derivative of the curve at P. Mathematically, we say that the slope at P = limh—>0 [f(x+h) - f(x)]÷h = df/dx, where h is the distance between P and Q, f(x) is the position of P, f(x+h) is the position of Q, and df/dx is the derivative of the curve with respect to x. The formula above is a specific case where the derivative is in terms of x and we're dealing with two dimensions. In physics, the instantaneous slope (derivative) of a position function is velocity, the derivative of velocity is acceleration, and the derivative of acceleration is jerk. Of course, the calculus formula P = limh—>0 [f(x+h) - f(x)]÷h = df/dx, where h is the distance between P and Q, f(x) is the position of P, f(x+h) is the position of Q, and df/dx is the derivative of the curve with respect to x was not used anywhere in your spreadsheet, so you are just bullshitting. Also, However, the slope of a bullet in flight is constantly changing, the deceleration is not constant, and the slope contains an infinite number of points. Moreover, you have merely bullshitted and have not described any formula to obtain the average velocity of the bullet over a given range, using instantaneous velocities. While you claim calculus formulas in your spreadsheet, you have yet to show a formula to sum changing parts of a spreadsheet column, i.e., sum row 1 and 2, sum row 1 thru 3, then row 1 thru 4, and so forth. I used such a formula and it showed that your column contained arithmetical errors not created by a spreadsheet formula. When you can program adding sums, I'll consider you doing calculus. As it is, you have not demostrated the ability to consistently add two numbers together, which is what you did to to sum that column. You added rows 1 and 2 to get the row 2 total; then you added row 3 to get the row 3 total, and so on, making two errors in 26 rows. You are fortunate it was now a thousand rows on a spreadsheet in a finance office. The formula for calculating average velocity (d/t) is given by the Khan Academy in the video you referenced. In their example, they divide a distance fo 1000m by 200s and get an average velocity of 5 m/s, and then they explicitly state, that siad result "doesn't necessarily equal the instantaneous velocities at particular points." The Khan Academy does not say that you can sum two instantaneous velocities and divide by two, and get an average velocity between the two points. See what you referenced. The first sentence is important — pretend you are a physics student. - [Instructor] Pretend you are a physics student. You are just getting out of class. You were walking home when you remembered that there was a Galaxy Wars marathon on tonight, so you'd do what every physics student would do: run. You're pretty motivated to get home, so say you start running at six meters per second. Maybe it's been a while since the last time you ran, so you have to slow down a little bit to two meters per second. When you get a little closer to home, you say: "No, Captain Antares wouldn't give up "and I'm not giving up either", and you start running at eight meters per second and you make it home just in time for the opening music. These numbers are values of the instantaneous speed. The instantaneous speed is the speed of an object at a particular moment in time. And if you include the direction with that speed, you get the instantaneous velocity. In other words, eight meters per second to the right was the instantaneously velocity of this person at that particular moment in time. Note that this is different from the average velocity. If your home was 1,000 meters away from school and it took you a total of 200 seconds to get there, your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip. In other words, let's say you jogged 60 meters in a time of 15 seconds. During this time you were speeding up and slowing down and changing your speed at every moment. Regardless of the speeding up or slowing down that took place during this path, your average velocity's still just gonna be four meters per second to the right; or, if you like, positive four meters per second. Just as your instantaneous velocity at two discrete and infinitesimal points can not be summed and divided by two to obtain average velocity, the instantaneous slope at two discrete and infinitesimal points will be different and cannot be used to calculate the slope of a traveling bullet whose velocity is contantly changing. While this bullshit about instantaneous slopes has diverted from your other bullshit about instantaneous velocities, you are still left searching to explain (1) your calculation used to derive average velocity over the specified distances, (2) your calculation used to change the formula for calculating average velocity over distance. Your chart stipulated distance and time. For 75 feet, you stipulated 0.02 seconds. This is your data, not mine. Using the formula, d/t=V(avg), that is 3,750 feet per second average velocity. If we assume that you meant the time to be anything between 0.015 and 0.025 seconds, that is 3000 - 5000 feet per second average velocity. For 1950 feet, you stipulated 0.86 seconds, and an average velocity of 2367.5926 feet per second, obtained by a formula you can neither present nor explain, nor can you provide any citation to any authority for your bullshit calculation. V(avg) = d/t = 1950/0.86 = 2267.4418 feet per second average velocity. If we assume that you meant the time to be anything between 0.855 and 0.865, then, V(avg) may equal 1950/0.0855 = 2280.7017 V(avg) may equal 1950/0.0865 = 2254.3353 Meanwhile, your bullshit 2367.5926 average velocity allows one to derive the time required to travel 1950 feet. 1950/2367.5926 = 0.823621429 seconds. Indeed, your second time for Tb, the time of the bullet, in your column E, reflects a bullet flight time of 0.823621 seconds, giving three less decimal points than I did, but rounding the the same precise thing at your chosen four decimal places, indicating how you derived that bullshit Tb from the bullshit average velocity. To check whether this bullshit time is not impossible with the stipulated data, one need only check if it is within the rounding possibilities of the stipulated data, i.e., from 0.855 to 0.865 seconds. Oh noes, your bullshit average velocity (0.823621) is not possible to reconcile with the stiplulated time, even allowing for the maximum rounding error. Your misbegotten time would round to 0.82 instead of 0.86. You have yet to explain how you can stipulate a bullet time of 0.86 seconds, and through the magic of VxH formulas, transform that time into 0.823621 seconds, and then use that visibly bullshit time to perform further bullshit calculations. If the bullet flew 1950 feet in 0.823621, why sure enough it went at an average velocity of 2367.5938 and covered 1950 feet. However, at the stipulated time of 0.86 seconds, at the bullshit average velocity of 2367.5938 feet per second, the bullet would have flown 2036.1307 feet. The stipulated distance is 1950 feet. At the maximum rounding down error to 0.855 seconds, at your bullshit average velocity of 2367.5926, the bullet would have flown 2024.292699 feet (0.855 x 2367.5926). The stipulated distance is 1950 feet. With your stipulated data, you may not have more or less than 1950 feet. You may not have less than 0.855 seconds flight time, nor more than 0.865 seconds flight time. You cannot change the distance the bullet flew, nor do more than consider a rounding error on the time. Your calculated numbers fail miserably. Your bullshit calculated numbers fall outside the maximum possible error attributable to a rounding error. Your bullshit calculations result in a new time, not within any rounding error, replacing 0.86 with 0.823621. Your bullshit average velocity over 1950 feet (2367.5926), at the maximum rounding error for stipulated time (0.86 rounded down to 0.855), requires the bullet to fly a minimum of 2024.292699 feet.
LOL. Idiot. ShooterCalculator.com Says: ======================== Professor DonkeyChan says: 1.2119 seconds nolu chan posted on 2017-10-30 19:58:41 ET https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53025&Disp=160#C160
Here is the ballistic data table generated for 1 yard intervals from 1875 to 1950 ft. Drag Function: G1 Wind Speed: 0 mph Corrected For Atmosphere Now tell us, Professor DonkeyChan - from the data provided, what is the average Velocity for the 75 ft segment ending at 1950 ft (1950ft, being the point at which, BTW, the instantaneous velocity is 1609fps)?
Meaningless waste of time that proves nothing.
2+2=4, Winstone.
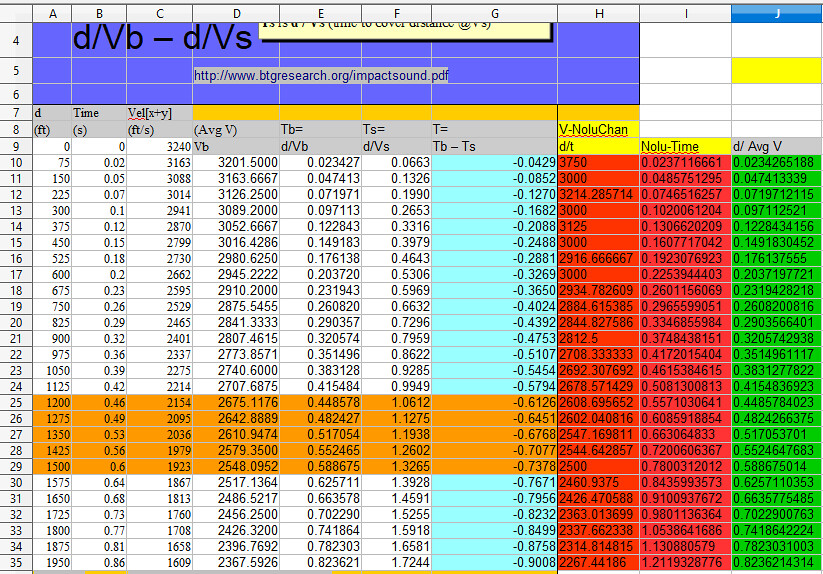
Column B of above spreadsheet shows the specified distance and the specified time for that distance. Column C shows the specified time for the distance traveled. Column D shows the time rounded down to the minimum time possibly explained by rounding. Column E shows the time rounded up to the maximum time possibly explained by rounding. Column F shows the Average Velocity (d/t) calculated with the unadjusted time from Column C. Column G shows the Average Velocity (d/t) calculated with the minimum time possible from Column D. This minimum time of flight shows the maximum possible average velocity of the bullet. Column H shows the Average Velocity (d/t) calculsted with the maximum time possible from Column E. This maximum time of flight show the minimum average velocity of the bullet. Column I shows the time for sound to travel the distance at 1130 fps. Column J shows the time difference between the bullet and the sound using unadjusted time from Column C. Column K shows the maximum possible time difference between the bullet and the sound using the time rounded down in Column D. Column L shows the minimum possible time difference between the bullet and the sound using the time rounded up in Column E. Column N states VXH Average Velocity using undisclosed math, presumably of Klingon origin. Column O states the instantaneous velocities at the distances specified in Column B. These velocities reflect a specific and infinitesimal point it time only, and do not describe velocity at any other point in time. Comparing Columns H and N, Column H calculates the maximum possible average velocity with the time round down as far is is possible. Column N is the average velocity claimed by VxH, using his secret Klingon mathematics. Notice his secret method obtain an average velocity well below the maximum possible for 75 feet, but comes nearer to the maximum possible with every calculation, and at 1200 feet his calculations leave the realm of the possible. At 1200 feet, at the specified time of 0.46 seconds, the average velocity would be 2608.70 feet per second (1200/0.46). Anyone can do the arithmetic. At 1200 feet, at 0.46 seconds rounded down as far as possible to 0.455 seconds (Column D), the maximum average veocity of 2637.36 feet per second (Column G) is achieved (2637.36/0.455). Anyone can still do the arithmetic. At this point, the VxH calculations exceed the possibilities of reality and achieve 2675.1176 feet per second. After this point, every VxH calculation widens the error. At 1950 feet, the Column G max average velocity is 2280.70 (1950/0.0855). After more calculations, the VxH error expands the difference to 2367.5926 feet per second. If carried on to further distances, the error will simply keep increasing. He started with 64% of the maximum possible average velocity, and surpassed 100% of the maximum on his 16th calculation, and continued to surpass the maximum possible average velocity by a greater and greater amount. Moreover, the distance and the time were a given.
...ft........ sec .... sec per VxH
75 0.02 0.023427
150 0.05 0.047413
225 0.07 0.071971
300 0.10 0.097113
375 0.12 0.122843
450 0.15 0.149183
525 0.18 0.176138
600 0.20 0.203720
675 0.23 0.231943
750 0.26 0.260820
825 0.29 0.290357
900 0.32 0.320574
975 0.36 0.351496
1050 0.39 0.383128
1125 0.42 0.415484
1200 0.46 0.448578
1275 0.49 0.482427
1350 0.53 0.517054
1425 0.56 0.552465
1500 0.60 0.588675
1575 0.64 0.625711
1650 0.68 0.663578
1725 0.73 0.702290
1800 0.77 0.741864
1875 0.81 0.782303
1950 0.86 0.082621
Notice how VxH, in his calculations, at and after 1200 feet, reduces the time of flight of the bullet by more than any possible amount of rounding from two decimal places. By 1950 feet, VxH has "rounded off" 0.86 and amazingly reduced the stated flight time to his own preferred 0.82621.
>>By 1950 feet, VxH has "rounded off" 0.86 Nope. Not a rounding error Super Genius. It's an artifact manufacted from the AVERAGING curve. >>preferred 0.82621. Nope. Try to keep up - - I've moved on with a revised curve that reconstructs time from Velocity and Distance, As per what I said in https://libertysflame.com/cgi-bin/readart.cgi? ArtNum=53046&Disp=105#C105 the next step in the quest is to explore methods of deriving Time relative to the slope of the DIFFERENCE between Vmin and Vmax for a given vector segment. So, Professor DonkeyChan -- Here is the ballistic data table generated for 1 yard intervals from 1875 to 1950 ft. Drag Function: G1 Wind Speed: 0 mph Corrected For Atmosphere
You have explored methods which require require rewriting the bullet flight times far beyond any possible rounding error. Reconstructing the given travel time is VxH BULLSHIT. Time and distance are given. Rounding the given time up or down does not help your bullshit work. Your bullshit methodology changes the given 0.86 seconds elapsed time to 0.82 seconds. There is no valid formula in the world for that. Time and distance are given data. Average velocity equals distance divided by time. Distance in feet, divideded by time in seconds, yields velocity in feet per second. Column B of above spreadsheet shows the specified distance and the specified time for that distance. Column C shows the specified time for the distance traveled. Column D shows the time rounded down to the minimum time possibly explained by rounding. Column E shows the time rounded up to the maximum time possibly explained by rounding. Column F shows the Average Velocity (d/t) calculated with the unadjusted time from Column C. Column G shows the Average Velocity (d/t) calculated with the minimum time possible from Column D. This minimum time of flight shows the maximum possible average velocity of the bullet. Column H shows the Average Velocity (d/t) calculsted with the maximum time possible from Column E. This maximum time of flight show the minimum average velocity of the bullet. Column I shows the time for sound to travel the distance at 1130 fps. Column J shows the time difference between the bullet and the sound using unadjusted time from Column C. Column K shows the maximum possible time difference between the bullet and the sound using the time rounded down in Column D. Column L shows the minimum possible time difference between the bullet and the sound using the time rounded up in Column E. Column N states VXH Average Velocity using undisclosed math, presumably of Klingon origin. Column O states the instantaneous velocities at the distances specified in Column B. There velocities reflect a specific and infinitesimal point it time only, and do not describe velocity at any other point in time. Comparing Columns H and N, Column H calculates the maximum possible average velocity with the time round down as far is is possible. Column N is the average velocity claimed by VxH, using his secret Klingon mathematics. Notice his secret method obtain an average velocity well below the maximum possible for 75 feet, but comes nearer to the maximum possible with every calculation, and at 1200 feet his calculations leave the realm of the possible. At 1200 feet, at the specified time of 0.46 seconds, the average velocity would be 2608.70 feet per second (1200/0.46). Anyone can do the arithmetic. At 1200 feet, at 0.46 seconds rounded down as far as possible to 0.455 seconds (Column D), the maximum average veocity of 2637.36 feet per second (Column G) is achieved (2637.36/0.455). Anyone can still do the arithmetic. At this point, the VxH calculations exceed the possibilities of reality and achieve 2675.1176 feet per second. After this point, every VxH calculation widens the error. At 1950 feet, the Column G max average velocity is 2280.70 (1950/0.0855). After more calculations, the VxH error expands the difference to 2367.5926 feet per second. If carried on to further distances, the error will simply keep increasing. He started with 64% of the maximum possible average velocity, and surpassed 100% of the maximum on his 16th calculation, and continued to surpass the maximum possible average velocity by a greater and greater amount. Moreover, the distance and the time were a given.
ft.......... sec..... sec
75 0.02 0.023427
150 0.05 0.047413
225 0.07 0.071971
300 0.10 0.097113
375 0.12 0.122843
450 0.15 0.149183
525 0.18 0.176138
600 0.20 0.203720
675 0.23 0.231943
750 0.26 0.260820
825 0.29 0.290357
900 0.32 0.320574
975 0.36 0.351496
1050 0.39 0.383128
1125 0.42 0.415484
1200 0.46 0.448578
1275 0.49 0.482427
1350 0.53 0.517054
1425 0.56 0.552465
1500 0.60 0.588675
1575 0.64 0.625711
1650 0.68 0.663578
1725 0.73 0.702290
1800 0.77 0.741864
1875 0.81 0.782303
1950 0.86 0.082621
Notice how VxH, in his calculations, at and after 1200 feet, reduces the time of flight of the bullet by more than any possible amount of rounding from two decimal places. By 1950 feet, VxH has "rounded off" 0.86 and amazingly calculated, by secret methodology, the stated flight time to his own preferred 0.82621. That is VxH bullshit. Not only wrong but impossible on its face. Now tell us, Professor DonkeyChan - from the data provided, what is the average Velocity for the 75 ft segment ending at 1950 ft (1950ft, being the point at which, BTW, the instantaneous velocity is 1609fps)? The average velocity of any object covering 1950 feet in 0.86 seconds is 1950/0.86 = 2267.4419 feet per second. It could be a flying refrigerator. If it goes 1950 feet in 0.86 seconds, the average velocity is 2267.4419 seconds. The object could have sped up and slowed down between 0 and 1950 feet in any manner and it makes no difference. If the object covers the 1950 feet in 0.86 seconds, the average velocity for the 1950 foot distance is 2267.4419 seconds. Recall the Khan Academy video you previously referenced: - [Instructor] Pretend you are a physics student. You are just getting out of class. You were walking home when you remembered that there was a Galaxy Wars marathon on tonight, so you'd do what every physics student would do: run. You're pretty motivated to get home, so say you start running at six meters per second. Maybe it's been a while since the last time you ran, so you have to slow down a little bit to two meters per second. When you get a little closer to home, you say: "No, Captain Antares wouldn't give up "and I'm not giving up either", and you start running at eight meters per second and you make it home just in time for the opening music. These numbers are values of the instantaneous speed. The instantaneous speed is the speed of an object at a particular moment in time. And if you include the direction with that speed, you get the instantaneous velocity. In other words, eight meters per second to the right was the instantaneously velocity of this person at that particular moment in time. Note that this is different from the average velocity. If your home was 1,000 meters away from school and it took you a total of 200 seconds to get there, your average velocity would be five meters per second, which doesn't necessarily equal the instantaneous velocities at particular points on your trip. In other words, let's say you jogged 60 meters in a time of 15 seconds. During this time you were speeding up and slowing down and changing your speed at every moment. Regardless of the speeding up or slowing down that took place during this path, your average velocity's still just gonna be four meters per second to the right; or, if you like, positive four meters per second. [snip] The instantaneous velocity at 1950 feet is irrelevant to the calculation of the average velocity over the range 0 to 1950 feet.
LOL. It's not a rounding error Professor DonkeyChan. How you coming along with that Average Velocity for the 75 foot segment ending at 1950 ft?
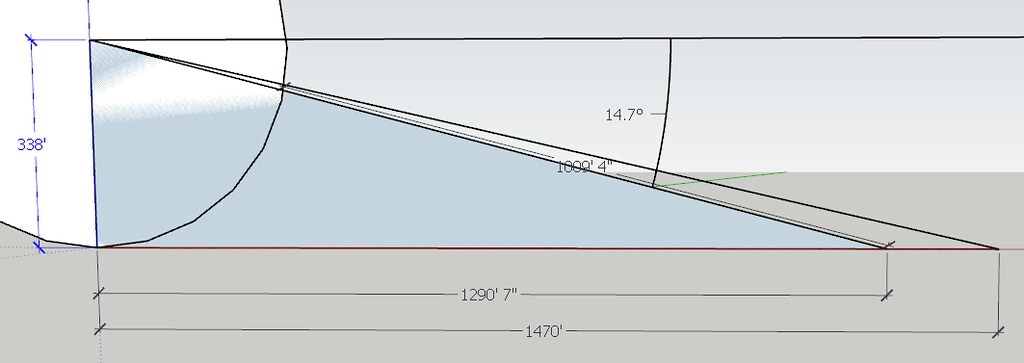
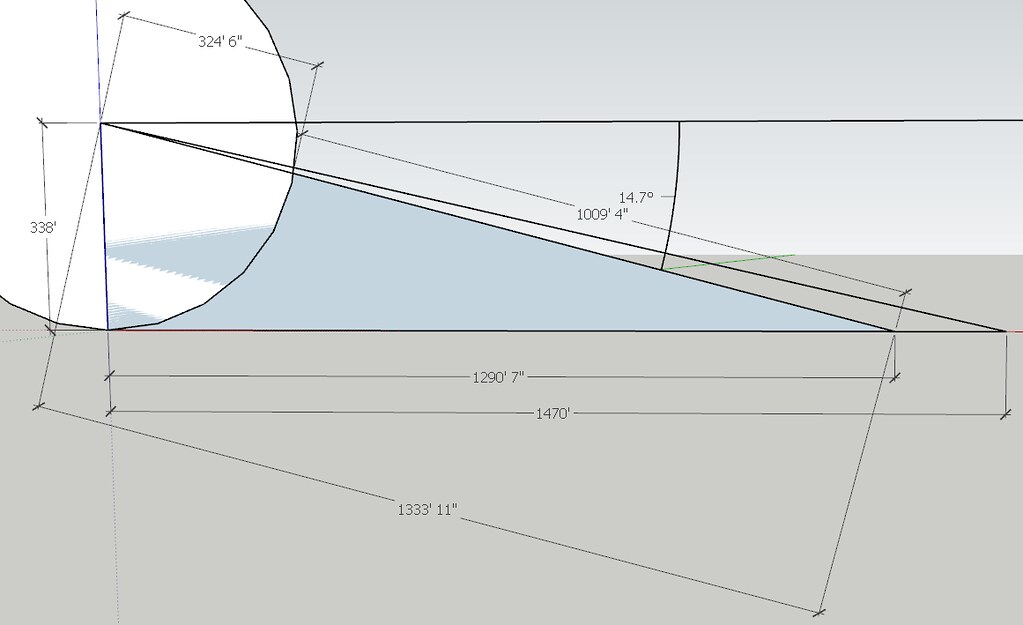
It came along quite well. Anything that travels 1950 feet in 1.06 seconds travels an average velocity of 2122.64 feet per second. The formula is distance divided by time. How are you coming along with your bullet going splat at ~520 feet ground distance from Mandalay Bay? How did you work out that negative 33º angle? Side a represents the vertical height of Paddock's vantage point. At the 32nd floor, and at 10.9 feet per floor, (32-1) x 10.9 = 338 feet. The VxH specified shooting angle was -33°. This should probably be expressed as a positive angle of declination. Not all ballistic calculators will even accept a negative angle value, but specify 0 to 90 degrees. For another calculator, see: http://gundata.org/blog/post/223-ballistics-chart/ It appears that VxH drew an imaginary horizontal line d at a vertical height of 338 feet from the ground, and an imaginary 338 foot line e down to the ground, bringing into view a rectangle with a mirror image triangle to that above. VxH guessed 33º as the acute angle formed at the junction of sides c and imaginary side d at point B. VxH guessed very wrongly. With a specified shooting angle of 33º at the junction of lines c and d, the angle made by sides c and b would also be 33º, and angle ß, made by sides a and c would be 57º. (The right angle at point A is 90º. The other two angles must add up to 90º.) With side a being 338 feet, side b would be 520.4743578 feet, and side c would be 620.5944 feet. As may be seen, disregarding gravity, if the bullet flew downward at the specified 33º from a height of 338 feet, it would fly a straight line of sight path into the ground at ~520 feet from the Mandalay Bay at ground level. Calculating the bullet velocity after that point may be difficult, even with secret Klingon math.
>>The formula is distance divided by time. And when you don't have data for time with enough precision - what then, professor Donkeychan? Drag Function: G1 Wind Speed: 0 mph Corrected For Atmosphere
BZZZT! Probably not, since using 0.33 instead of -0.33 produces a slower velocity: (0.33) 1950 0.89 1489 (-0.33) 1950 0.86 1609
VxH guessed 33º as the acute angle formed at the junction of sides c and imaginary side d at point B. VxH guessed very wrongly. Yep. You're almost right - I've been meaning to take another look at the angle with a model in Google Sketchup... which says At 1290' from a height of 338' is -14.7 But the reconstructed time could still more more accurate. Any luck figuring that CURVE out?
BZZZT! Probably not, since using 0.33 instead of -0.33 produces a slower velocity: There is no 33 degree angle involved. Using your trajectory, Paddock would have come closer to shooting off his big toe than hitting anywhere in the festival venue. Learn to read: Declination is downward. Negative 33 degrees inclination is the same as 33 degrees declination. It is the difference between your preferred -33 degrees upward and 33 degrees downward. 33 degrees downward points down. Negative 33 degrees downward points up. It is like walking negative 33 feet east is walking 33 feet west. For another calculator, see: The gundata entry specifies "Shooting angle (0..89)." Stick a negative value in there and it will reject. As there is no such thing as a triangle with negative angles, the values for every angle of a triangle are positive values. In a triangle with sides -3 and -4, a2 + b2 = c2 would yield a hypotenuse of positive 5. (0.33) 1950 0.89 1489 (-0.33) 1950 0.86 1609 The data available at the links shows the only data change between my two charts is one is -33 and the other is 33. Not so for the chart you just created with yet another time calculation. You changed the input data. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=75dcb734 -33 degrees http://www.shooterscalculator.com/images/trajectory/ballistic_trajectory_chart_75dcb734.png This chart made with the original -33 data, shows the bullet rise above the original altitude, and remain above that altitude, for over 300 yards. This is an amazing feat for a bullet shot on a steep downward angle. - - - - - - - - - - http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=fd15e1b9 33 degrees http://www.shooterscalculator.com/images/trajectory/ballistic_trajectory_chart_fd15e1b9.png Amazingly, when the angle is changed from -33 to 33, the flight path does not change, according to your calculator. - - - - - - - - - - When your calculator permits you to enter ridiculous data, it provides you with ridiculous results. As one may observe, it provides the precise same flight trajectory, whether at 33 or -33. When fired at 33 degrees downward, the bullet goes upward and remains above the original location for over 300 yards. The data available at the links shows the only data change to be -33 to 33. The time for 650 yards/1950 feet is 0.86 in either instance. The average velocity for any object that travels 1950 feet in 0.86 seconds is 1950/0.86 = 2267.4418 ft/sec. - - - - - - - - - - YOUR DATA WITH A NEW TIME SHOWS YOU ALTERED THE INPUT DATA. And your flight trajectory chart for -33 degrees featuring a new time http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=81e7edd6 http://www.shooterscalculator.com/images/trajectory/ballistic_trajectory_chart_81e7edd6.png Notice that with the projectile purported fired at a 33 degree downward angle, the projectile maintains its original altitude for about 150 yards. Of course, in your derivation of data, you changed the properties of the chart: Drag Function: G1 Corrected For Atmosphere - - - - - - - - - - - - - - - - - - - - To see the prior input data, just look: As for your magic ability to fire rounds down at 33º, and have them either rise or maintain altitude for hundreds of yards,
Yep. You're almost right - I've been meaning to take another look at the angle with a model in Google Sketchup... which says At 1290' from a height of 338' is -14.7 Damn, you are more screwed up than I thought. Now you are presenting a triangle with side a being 338 feet, side b being 1290 feet 7 inches (1290.5833 ft), and an hypotenuse of 1009 ft 4 in. I positively can't remember the last triangle I saw where the hypotenuse was shorter than one of the sides. Your Klingon math is magic, and Google Sketchup is a miracle worker. If side a is 338 ft, and the angle of elevation of 14.7º rises to that height of 338 ft, side b will be 1264.283557 feet. So, the hypotenuse is impossible, and side b is whack by 26 feet. If the angle of elevation is 14.7 degrees, and the range is 1290' 7", then the height would be 345.0311072 feet and each floor would be over 11 feet. Put down Google sketch and pick up a scientific calculator and do some trigonometry. You can actually get correct results with trig. You are supposed to be dazzling me with your math skills, not some shit like Google Sketchup. Google Sketchup? Really?
And when you don't have data for time with enough precision - what then, professor Donkeychan? By the way, if the given time and distance data was imprecise, what was used to calculate the instantaneous velocities? [VxH at #175] LOL. It's not a rounding error Professor DonkeyChan. If the given data is not subject to a rounding error, then it is totally accurate and precise, distance/time works fine, and your bogus calculated data is bullshit. If the given data is subject to a rounding error, then it is accurate ± 0.005, in which case using distance/time works to define the possible range of average velocity within the rounding factor, and this also proves your bogus calculated data is bullshit.
If the given data is not subject to a rounding error, then it is totally accurate and precise, distance/time works fine, and your bogus calculated data is bullshit. It's still not a rounding error, Super Genius. It's a result of the AVERAGING calculation that was used in the context of Time data that was truncated to an insufficiently precise (for the purpose of determining average velocity) 2 decimal points. =SUM(C9:C10)/L9
Pssst. Professor DonkeyChan. 1009 ft 4 in is the distance from the radius of that circle. LOL. FAIL again vociferously pretentious NoluBUFFOON!
LOL. Do the Math, Professor DonkeyDung. I didn't rescale the circle for the purpose of determining the angle. So - No bigee with the radius 324' 6" - the dimensions still add up for the hypotenuse.
Really!

#148. To: nolu chan, A K A Stone (#147)
#149. To: nolu chan (#147)
(Edited)
To calculate the average velocity of the bullet, divide distance by time.

#150. To: VxH (#148)
Even without the ballistic data (which is calculated correctly for the parameters entered)
#151. To: nolu chan (#150)
(Edited)
#152. To: nolu chan (#147)
(Edited)
Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
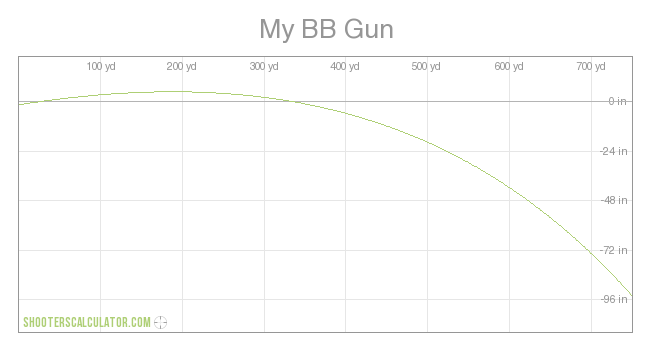
Speed of Sound: 1130 fpsRange Time Vel[x+y] (ft) (s) (ft/s) 0 0.00 3240 75 0.02 3163 150 0.05 3088 225 0.07 3014 300 0.10 2941 375 0.12 2870 450 0.15 2799 525 0.18 2730 600 0.20 2662 675 0.23 2595 750 0.26 2529 825 0.29 2465 900 0.32 2401 975 0.36 2337 1050 0.39 2275 1125 0.42 2214 1200 0.46 2154 1275 0.49 2095 1350 0.53 2036 1425 0.56 1979 1500 0.60 1923 1575 0.64 1867 1650 0.68 1813 1725 0.73 1760 1800 0.77 1708 1875 0.81 1658 1950 0.86 1609 2025 0.91 1561 2100 0.96 1515 2175 1.01 1470 2250 1.06 1426 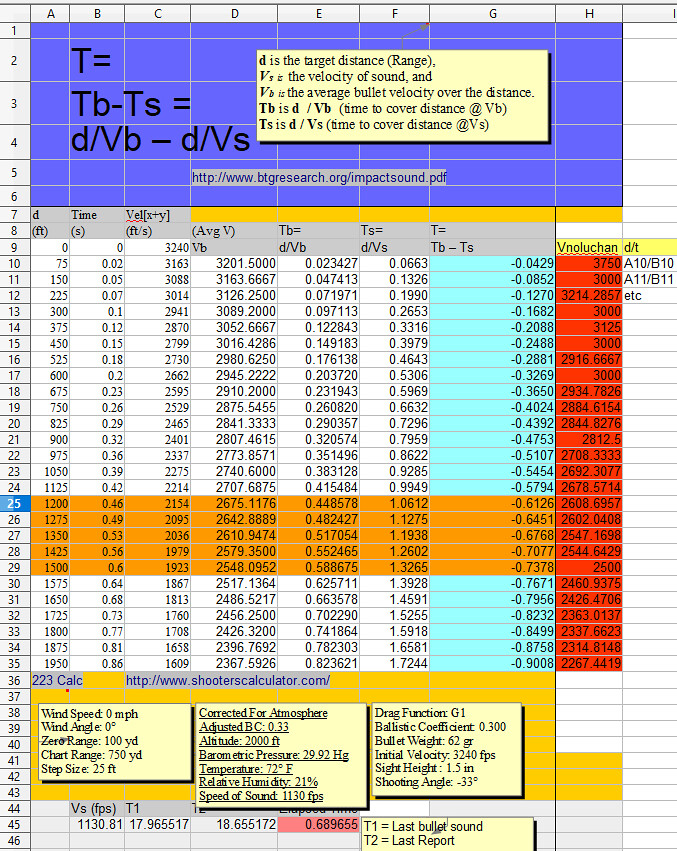

#153. To: VxH (#151)
[Vxh #148] Even without the ballistic data (which is calculated correctly for the parameters entered)
Keep in mind this is an approximation....
As for column 3, "Vel[x+y] (ft/s)", you seem to have forgotten to give any definition of x or y on your chart.
#154. To: nolu chan (#153)
(Edited)
divide the distance by the velocity and get the time to more decimal places and eliminate the rounding error.

"Vel[x+y] (ft/s)", you seem to have forgotten to give any definition of x or y on your chart.
#155. To: VxH (#154)
So you're going to drive 99 miles at 2mph, then drive and 1 mile at 100mph.
0.023427s after 75 feet
0.047413s after 150 feet.
0.0237116s - 075 ft [d/Vb]
0.0485751s - 150 ft [d/Vb] LOL. I know what they mean on the Ballistic calculator. Don't you?
And speaking of Vectors: If we treated each 75 ft segment as a vector and then calculated time as a function of the relationship between 75ft and the difference between {Vn..Vn+1}... that might work a little better than your simple d/v idea.
Vs is the velocity of sound, and
Vb is the average bullet velocity over the distance
Tb is d / Vb (time to cover distance @ Vb)
Ts is d/Vs (time to cover distance @Vs)
#156. To: nolu chan (#155)
You still did not explain why you used Vel[x+y] rather than Vel[x].
#157. To: nolu chan (#155)
(Edited)
#158. To: nolu chan (#155)
(Edited)
Column J: d/Avg V
Why is that?
#159. To: All (#154)

#160. To: VxH, A K A Stone (#159)
speaking of Vectors...
BALLISTICS DATA SPREADSHEET
A1 AVERAGE VELOCITY AND TIME DIFF OVER TOTAL DISTANCE AVERAGE VELOCITY FOR EACH 75 FEET SEGMENT 2 3 B C D E F G H I J K L 4 d Time (avg) Vel[x+y] Ts=d/Vs T=Tb - Ts Tb 75 ft Avg Velocity for Segment Segment Segment 5 (ft) d/Vel[x+y] (ft/s) d/Vs ABS(Tb-Ts) +C7-C6 75 foot segment distance begin end 6 0 0.0000 3240 +75/H4 +B7-B6 +K7+75 A7 7 75 0.0237 3163 0.0664 0.0427 0.0237 3163.0000 75 0 75 8 150 0.0486 3088 0.1327 0.0842 0.0249 3016.4744 75 75 150 9 225 0.0747 3014 0.1991 0.1245 0.0261 2876.1533 75 150 225 10 300 0.1020 2941 0.2655 0.1635 0.0274 2741.7798 75 225 300 11 375 0.1307 2870 0.3319 0.2012 0.0287 2617.2620 75 300 375 12 450 0.1608 2799 0.3982 0.2375 0.0301 2490.8930 75 375 450 13 525 0.1923 2730 0.4646 0.2723 0.0315 2378.2353 75 450 525 14 600 0.2254 2662 0.5310 0.3056 0.0331 2266.7686 75 525 600 15 675 0.2601 2595 0.5973 0.3372 0.0347 2160.0657 75 600 675 16 750 0.2966 2529 0.6637 0.3672 0.0364 2057.9351 75 675 750 17 825 0.3347 2465 0.7301 0.3954 0.0381 1967.1773 75 750 825 18 900 0.3750 2400 0.7965 0.4215 0.0403 1860.3774 75 825 900 19 975 0.4172 2337 0.8628 0.4456 0.0422 1777.1863 75 900 975 20 1050 0.4615 2275 0.9292 0.4677 0.0443 1691.5924 75 975 1050 21 1125 0.5081 2214 0.9956 0.4874 0.0466 1609.7315 75 1050 1125 22 1200 0.5571 2154 1.0619 0.5048 0.0490 1531.4566 75 1125 1200 23 1275 0.6089 2094 1.1283 0.5194 0.0518 1448.4509 75 1200 1275 24 1350 0.6631 2036 1.1947 0.5316 0.0542 1384.2156 75 1275 1350 25 1425 0.7201 1979 1.2611 0.5410 0.0570 1315.8863 75 1350 1425 26 1500 0.7800 1923 1.3274 0.5474 0.0600 1250.6135 75 1425 1500 27 1575 0.8436 1867 1.3938 0.5502 0.0636 1179.8360 75 1500 1575 28 1650 0.9101 1813 1.4602 0.5501 0.0665 1127.9144 75 1575 1650 29 1725 0.9801 1760 1.5265 0.5464 0.0700 1071.1245 75 1650 1725 30 1800 1.0539 1708 1.5929 0.5391 0.0738 1016.9418 75 1725 1800 31 1875 1.1309 1658 1.6593 0.5284 0.0770 973.8184 75 1800 1875 32 1950 1.2119 1609 1.7257 0.5137 0.0811 925.3285 75 1875 1950 33 2025 1.2972 1561 1.7920 0.4948 0.0853 879.1211 75 1950 2025 34 2100 1.3861 1515 1.8584 0.4723 0.0889 843.7085 75 2025 2100 35 2175 1.4796 1470 1.9248 0.4452 0.0935 802.5405 75 2100 2175 36 2250 1.5778 1426 1.9912 0.4133 0.0982 763.3722 75 2175 2250 37 38 Total 39 1.5780 40 SUM G7:G36
#161. To: nolu chan, A K A Stone (#160)
4 d Time (avg) Vel[x+y] 5 (ft) d/Vel[x+y] (ft/s) 32 1950 1.2119 1609 1950 0.86 1609 Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%Range Time Vel[x+y] (ft) (s) (ft/s) 0 0.00 3240 75 0.02 3163 150 0.05 3088 225 0.07 3014 300 0.10 2941 375 0.12 2870 450 0.15 2799 525 0.18 2730 600 0.20 2662 675 0.23 2595 750 0.26 2529 825 0.29 2465 900 0.32 2401 975 0.36 2337 1050 0.39 2275 1125 0.42 2214 1200 0.46 2154 1275 0.49 2095 1350 0.53 2036 1425 0.56 1979 1500 0.60 1923 1575 0.64 1867 1650 0.68 1813 1725 0.73 1760 1800 0.77 1708 1875 0.81 1658 1950 0.86 1609 2025 0.91 1561 2100 0.96 1515 2175 1.01 1470 2250 1.06 1426
#162. To: VxH (#161)
#163. To: A K A Stone, NoluChan (#162)
(Edited)
4 d Time (avg) Vel[x+y] 5 (ft) d/Vel[x+y] (ft/s) 32 1950 1.2119 1609
#164. To: VxH, A K A Stone (#161)
How'd ya manage to do that, Professor DonkyChan?
#165. To: A K A Stone, VxH (#162)
I have one question. You keep changing your numbers. But they still always fit with your pet theory. Why is that
[VxH] Ballistic deceleration is a non-linear system. Calculations we're using to model the system are thus only approximations. Different functions and methods can be used to model the system with varying degrees of approximation.
Video transcript
#166. To: nolu chan, A K A Stone (#164)
(Edited)
Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%1950 0.86 1609 4 d Time (avg) Vel[x+y] 5 (ft) d/Vel[x+y] (ft/s) 32 1950 1.2119 1609 
#167. To: VxH (#166)
Meanwhile...
Answer byBlue
Confidence votes 38.3K When Q gets extremely close to P (so that there is an infinitesimal space between P and Q), then the slope of the secant line approximates the slope at P. When we take the limit of that tiny distance as it approaches zero (meaning we make the space disappear) we get the slope of the curve at P. This is the instantaneous slope or the derivative of the curve at P.
Video transcript
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
#168. To: nolu chan (#167)
(Edited)

Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%1950 0.86 1609 4 d Time (avg) Vel[x+y] 5 (ft) d/Vel[x+y] (ft/s) 32 1950 1.2119 1609
#169. To: nolu chan, A K A Stone, TooConservative (#167)
(Edited)
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 1000 yd
Maximum Range: 50002 yd
Step Size: 1 yd
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
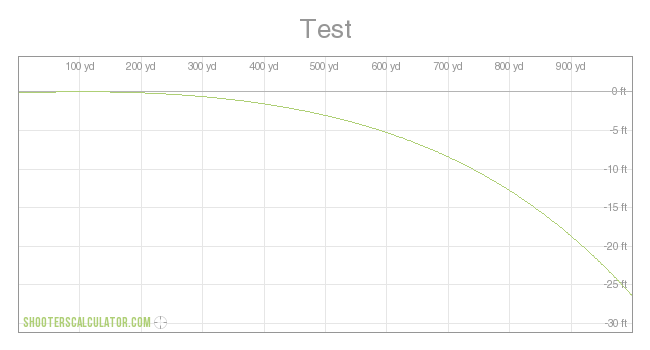
Speed of Sound: 1130 fps Range Time Vel[x+y] (ft) (s) (ft/s) 1875 0.81 1658 1878 0.81 1656 1881 0.82 1654 1884 0.82 1652 1887 0.82 1650 1890 0.82 1648 1893 0.82 1646 1896 0.83 1644 1899 0.83 1642 1902 0.83 1640 1905 0.83 1638 1908 0.83 1636 1911 0.83 1634 1914 0.84 1632 1917 0.84 1630 1920 0.84 1628 1923 0.84 1626 1926 0.84 1624 1929 0.85 1622 1932 0.85 1621 1935 0.85 1619 1938 0.85 1617 1941 0.85 1615 1944 0.86 1613 1947 0.86 1611 1950 0.86 1609
#170. To: VxH (#169)
#171. To: A K A Stone (#170)
(Edited)
#172. To: VxH, A K A Stone (#169)
Unresponsive obfuscatory yukonesque bullshit
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
Distance and time specified Time rounded to plus or minus maximum Avg velocity Avg velocity Avg velocity time for sound ABS Tb - Ts ABS Tb - Ts ABS Tb - Ts time as given max possible min possible to travel dist time as given max possible min possible B C D E F G H I J K L N O P d Time Time -.005 Time +.005 Avg Vel unadj Avg Vel max Avg Vel min t for sound ABS Tdiff unadj ABS Tdiff MAX ABS Tdiff MIN VxH Avg Vel VxH Instant VxH Tdiff (ft) (seconds) (seconds) b/c b/d b/e b/1130 ABS(c8-i8) ABS(d8-i8) ABS(E8-I8) Velocity Tb-Ts 7 0 0.00 3240 8 75 0.02 0.015 0.025 3750.00 5000.00 3000.0000 0.0664 0.0464 0.0514 0.0414 3201.5000 3163 0.0429 9 150 0.05 0.045 0.055 3000.00 3333.33 2727.2727 0.1327 0.0827 0.0877 0.0777 3163.6667 3088 0.0852 10 225 0.07 0.065 0.075 3214.29 3461.54 3000.0000 0.1991 0.1291 0.1341 0.1241 3126.2500 3014 0.1270 11 300 0.10 0.095 0.105 3000.00 3157.89 2857.1429 0.2655 0.1655 0.1705 0.1605 3089.2000 2941 0.1682 12 375 0.12 0.115 0.125 3125.00 3260.87 3000.0000 0.3319 0.2119 0.2169 0.2069 3052.6667 2870 0.2088 13 450 0.15 0.145 0.155 3000.00 3103.45 2903.2258 0.3982 0.2482 0.2532 0.2432 3016.4286 2799 0.2488 14 525 0.18 0.175 0.185 2916.67 3000.00 2837.8378 0.4646 0.2846 0.2896 0.2796 2980.6250 2730 0.2881 15 600 0.20 0.195 0.205 3000.00 3076.92 2926.8293 0.5310 0.3310 0.3360 0.3260 2945.2222 2662 0.3269 16 675 0.23 0.225 0.235 2934.78 3000.00 2872.3404 0.5973 0.3673 0.3723 0.3623 2910.2000 2595 0.3650 17 750 0.26 0.255 0.265 2884.62 2941.18 2830.1887 0.6637 0.4037 0.4087 0.3987 2875.5455 2529 0.4024 18 825 0.29 0.285 0.295 2844.83 2894.74 2796.6102 0.7301 0.4401 0.4451 0.4351 2841.3333 2465 0.4392 19 900 0.32 0.315 0.325 2812.50 2857.14 2769.2308 0.7965 0.4765 0.4815 0.4715 2807.4615 2401 0.4753 20 975 0.36 0.355 0.365 2708.33 2746.48 2671.2329 0.8628 0.5028 0.5078 0.4978 2773.8571 2337 0.5107 21 1050 0.39 0.385 0.395 2692.31 2727.27 2658.2278 0.9292 0.5392 0.5442 0.5342 2740.6000 2275 0.5454 22 1125 0.42 0.415 0.425 2678.57 2710.84 2647.0588 0.9956 0.5756 0.5806 0.5706 2707.6875 2214 0.5794 23 1200 0.46 0.455 0.465 2608.70 2637.36 2580.6452 1.0619 0.6019 0.6069 0.5969 2675.1176 2154 0.6260 24 1275 0.49 0.485 0.495 2602.04 2628.87 2575.7576 1.1283 0.6383 0.6433 0.6333 2642.8889 2095 0.6451 25 1350 0.53 0.525 0.535 2547.17 2571.43 2523.3645 1.1947 0.6647 0.6697 0.6597 2610.9474 2036 0.6768 26 1425 0.56 0.555 0.565 2544.64 2567.57 2522.1239 1.2611 0.7011 0.7061 0.6961 2579.3500 1979 0.7077 27 1500 0.60 0.595 0.605 2500.00 2521.01 2479.3388 1.3274 0.7274 0.7324 0.7224 2548.0952 1923 0.7378 28 1575 0.64 0.635 0.645 2460.94 2480.31 2441.8605 1.3938 0.7538 0.7588 0.7488 2517.1364 1867 0.7671 29 1650 0.68 0.675 0.685 2426.47 2444.44 2408.7591 1.4602 0.7802 0.7852 0.7752 2486.5217 1813 0.7956 30 1725 0.73 0.725 0.735 2363.01 2379.31 2346.9388 1.5265 0.7965 0.8015 0.7915 2456.2500 1760 0.8232 31 1800 0.77 0.765 0.775 2337.66 2352.94 2322.5806 1.5929 0.8229 0.8279 0.8179 2426.3200 1708 0.8499 32 1875 0.81 0.805 0.815 2314.81 2329.19 2300.6135 1.6593 0.8493 0.8543 0.8443 2395.7692 1658 0.8758 33 1950 0.86 0.855 0.865 2267.44 2280.70 2254.3353 1.7257 0.8657 0.8707 0.8607 2367.5926 1609 0.9008 34 2025 0.91 0.905 0.915 2225.27 2237.57 2213.1148 1.7920 0.8820 0.8870 0.8770 35 2100 0.96 0.955 0.965 2187.50 2198.95 2176.1658 1.8584 0.8984 0.9034 0.8934 36 2175 1.01 1.005 1.015 2153.47 2164.18 2142.8571 1.9248 0.9148 0.9198 0.9098 37 2250 1.06 1.055 1.065 2122.64 2132.70 2112.6761 1.9912 0.9312 0.9362 0.9262
....d ........ t ... Vxh
#173. To: nolu chan (#172)
(Edited)

Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 1000 yd
Maximum Range: 50002 yd
Step Size: 1 yd
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fps Range Time Vel[x+y] (ft) (s) (ft/s) 1875 0.81 1658 1878 0.81 1656 1881 0.82 1654 1884 0.82 1652 1887 0.82 1650 1890 0.82 1648 1893 0.82 1646 1896 0.83 1644 1899 0.83 1642 1902 0.83 1640 1905 0.83 1638 1908 0.83 1636 1911 0.83 1634 1914 0.84 1632 1917 0.84 1630 1920 0.84 1628 1923 0.84 1626 1926 0.84 1624 1929 0.85 1622 1932 0.85 1621 1935 0.85 1619 1938 0.85 1617 1941 0.85 1615 1944 0.86 1613 1947 0.86 1611 1950 0.86 1609
Now tell us, Professor DonkeyChan - from the data provided, what is the average Velocity for the 75 ft segment ending at 1950 ft (1950ft, being the point at which, BTW, the instantaneous velocity is 1609fps)?
#174. To: VxH, A K A Stone (#173)
[VxH # 173] Nope. Try to keep up - - I've moved on with a revised curve that reconstructs time from Velocity and Distance,
YOUR CALCULATED DATA IS ALL BULLSHIT, AS ARE YOU
WHY IS YOUR CALCULATED DATA OUTSIDE THE POSSIBLE LIMITS OF A TIME ROUNDING ERROR???
Distance and time specified Time rounded to plus or minus maximum Avg velocity Avg velocity Avg velocity time for sound ABS Tb - Ts ABS Tb - Ts ABS Tb - Ts time as given max possible min possible to travel dist time as given max possible min possible B C D E F G H I J K L N O P d Time Time -.005 Time +.005 Avg Vel unadj Avg Vel max Avg Vel min t for sound ABS Tdiff unadj ABS Tdiff MAX ABS Tdiff MIN VxH Avg Vel VxH Instant VxH Tdiff (ft) (seconds) (seconds) b/c b/d b/e b/1130 ABS(c8-i8) ABS(d8-i8) ABS(E8-I8) Velocity Tb-Ts 7 0 0.00 3240 8 75 0.02 0.015 0.025 3750.00 5000.00 3000.0000 0.0664 0.0464 0.0514 0.0414 3201.5000 3163 0.0429 9 150 0.05 0.045 0.055 3000.00 3333.33 2727.2727 0.1327 0.0827 0.0877 0.0777 3163.6667 3088 0.0852 10 225 0.07 0.065 0.075 3214.29 3461.54 3000.0000 0.1991 0.1291 0.1341 0.1241 3126.2500 3014 0.1270 11 300 0.10 0.095 0.105 3000.00 3157.89 2857.1429 0.2655 0.1655 0.1705 0.1605 3089.2000 2941 0.1682 12 375 0.12 0.115 0.125 3125.00 3260.87 3000.0000 0.3319 0.2119 0.2169 0.2069 3052.6667 2870 0.2088 13 450 0.15 0.145 0.155 3000.00 3103.45 2903.2258 0.3982 0.2482 0.2532 0.2432 3016.4286 2799 0.2488 14 525 0.18 0.175 0.185 2916.67 3000.00 2837.8378 0.4646 0.2846 0.2896 0.2796 2980.6250 2730 0.2881 15 600 0.20 0.195 0.205 3000.00 3076.92 2926.8293 0.5310 0.3310 0.3360 0.3260 2945.2222 2662 0.3269 16 675 0.23 0.225 0.235 2934.78 3000.00 2872.3404 0.5973 0.3673 0.3723 0.3623 2910.2000 2595 0.3650 17 750 0.26 0.255 0.265 2884.62 2941.18 2830.1887 0.6637 0.4037 0.4087 0.3987 2875.5455 2529 0.4024 18 825 0.29 0.285 0.295 2844.83 2894.74 2796.6102 0.7301 0.4401 0.4451 0.4351 2841.3333 2465 0.4392 19 900 0.32 0.315 0.325 2812.50 2857.14 2769.2308 0.7965 0.4765 0.4815 0.4715 2807.4615 2401 0.4753 20 975 0.36 0.355 0.365 2708.33 2746.48 2671.2329 0.8628 0.5028 0.5078 0.4978 2773.8571 2337 0.5107 21 1050 0.39 0.385 0.395 2692.31 2727.27 2658.2278 0.9292 0.5392 0.5442 0.5342 2740.6000 2275 0.5454 22 1125 0.42 0.415 0.425 2678.57 2710.84 2647.0588 0.9956 0.5756 0.5806 0.5706 2707.6875 2214 0.5794 23 1200 0.46 0.455 0.465 2608.70 2637.36 2580.6452 1.0619 0.6019 0.6069 0.5969 2675.1176 2154 0.6260 24 1275 0.49 0.485 0.495 2602.04 2628.87 2575.7576 1.1283 0.6383 0.6433 0.6333 2642.8889 2095 0.6451 25 1350 0.53 0.525 0.535 2547.17 2571.43 2523.3645 1.1947 0.6647 0.6697 0.6597 2610.9474 2036 0.6768 26 1425 0.56 0.555 0.565 2544.64 2567.57 2522.1239 1.2611 0.7011 0.7061 0.6961 2579.3500 1979 0.7077 27 1500 0.60 0.595 0.605 2500.00 2521.01 2479.3388 1.3274 0.7274 0.7324 0.7224 2548.0952 1923 0.7378 28 1575 0.64 0.635 0.645 2460.94 2480.31 2441.8605 1.3938 0.7538 0.7588 0.7488 2517.1364 1867 0.7671 29 1650 0.68 0.675 0.685 2426.47 2444.44 2408.7591 1.4602 0.7802 0.7852 0.7752 2486.5217 1813 0.7956 30 1725 0.73 0.725 0.735 2363.01 2379.31 2346.9388 1.5265 0.7965 0.8015 0.7915 2456.2500 1760 0.8232 31 1800 0.77 0.765 0.775 2337.66 2352.94 2322.5806 1.5929 0.8229 0.8279 0.8179 2426.3200 1708 0.8499 32 1875 0.81 0.805 0.815 2314.81 2329.19 2300.6135 1.6593 0.8493 0.8543 0.8443 2395.7692 1658 0.8758 33 1950 0.86 0.855 0.865 2267.44 2280.70 2254.3353 1.7257 0.8657 0.8707 0.8607 2367.5926 1609 0.9008 34 2025 0.91 0.905 0.915 2225.27 2237.57 2213.1148 1.7920 0.8820 0.8870 0.8770 35 2100 0.96 0.955 0.965 2187.50 2198.95 2176.1658 1.8584 0.8984 0.9034 0.8934 36 2175 1.01 1.005 1.015 2153.47 2164.18 2142.8571 1.9248 0.9148 0.9198 0.9098 37 2250 1.06 1.055 1.065 2122.64 2132.70 2112.6761 1.9912 0.9312 0.9362 0.9262
d ........ given..........Vxh bullshit
[VxH]
1950 0.86 1609
Video transcript
#175. To: nolu chan (#174)
beyond any possible rounding error
#176. To: VxH (#175)
How you coming along with that Average Velocity for the 75 foot segment ending at 1950 ft?
#177. To: nolu chan (#176)
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 1000 yd
Maximum Range: 50002 yd
Step Size: 1 yd
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fps Range Time Vel[x+y] (ft) (s) (ft/s) 1875 0.81 1658 1878 0.81 1656 1881 0.82 1654 1884 0.82 1652 1887 0.82 1650 1890 0.82 1648 1893 0.82 1646 1896 0.83 1644 1899 0.83 1642 1902 0.83 1640 1905 0.83 1638 1908 0.83 1636 1911 0.83 1634 1914 0.84 1632 1917 0.84 1630 1920 0.84 1628 1923 0.84 1626 1926 0.84 1624 1929 0.85 1622 1932 0.85 1621 1935 0.85 1619 1938 0.85 1617 1941 0.85 1615 1944 0.86 1613 1947 0.86 1611 1950 0.86 1609
#178. To: nolu chan (#176)
This should probably be expressed as a positive angle of declination.
#179. To: nolu chan (#176)
(Edited)
It appears that VxH drew an imaginary horizontal line d at a vertical height of 338 feet from the ground, and an imaginary 338 foot line e down to the ground, bringing into view a rectangle with a mirror image triangle to that above.

#180. To: VxH (#178)
This should probably be expressed as a positive angle of declination.
The VxH specified shooting angle was -33°. This should probably be expressed as a positive angle of declination. Not all ballistic calculators will even accept a negative angle value, but specify 0 to 90 degrees.
BZZZT! Probably not, since using 0.33 instead of -0.33 produces a slower velocity:
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°
Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd [Was 25 yd/75 feet]
Chart Range: 1000 yd[Was 750 yd]
Maximum Range: 50002 yd [Was 750 yd/2250 ft]
Step Size: 1 yd [Was 25 yd/75 ft]
Adjusted BC: 0.307 [was 0.300]
Altitude: 0 ft [was 2000 ft]
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fps 
#181. To: VxH, A K A Stone (#179)
VxH guessed 33º as the acute angle formed at the junction of sides c and imaginary side d at point B. VxH guessed very wrongly.

#182. To: VxH, A K A Stone (#177)
The formula is distance divided by time.
#183. To: nolu chan (#182)
[VxH at #175] LOL. It's not a rounding error Professor DonkeyChan.
=SUM(C$9:C11)/L10
=SUM(C$9:C12)/L11
etc.
Where column L contains 1 @ row 8 and =+ L8+1, =+L9+1 etc for rows 9..34
#184. To: nolu chan (#181)
(Edited)
and an hypotenuse of 1009 ft 4 in.
#185. To: nolu chan, A K A Stone (#181)
(Edited)
#186. To: nolu chan (#181)
(Edited)
Google Sketchup? Really?
Top • Page Up • Full Thread • Page Down • Bottom/Latest
[Home] [Headlines] [Latest Articles] [Latest Comments] [Post] [Mail] [Sign-in] [Setup] [Help] [Register]
